Почему именно с ранга 2. Я сначала попробовал с ранга 1. Правильно ли я понимаю, что в данном случае кривизна нулевая, и

?
Да, и поэтому этот случай тривиален: "нулевой класс Понтрягина" никакой информации не несёт, потому что он всегда 1.
Ну это, вроде, понимаю: на тривиализующих окрестностях выбираем скалярное, и потом с помощью разбиения единицы склеиваем на всем многообразии. Так?
Да.
Из теоремы Леви-Чевиты?
Теорема Леви-Чивиты (та, которую я знаю) -- это про касательное расслоение, и сложность там в том, чтобы не было кручения. Нам неважно, будет ли кручение, поэтому всё проще. И не надо угадывать.
Множество 2-форм на

в окрестности

, то есть

(это то же самое, что Вы написали?)? Но почему

?
Кривизна -- это, действительно, элемент

. Теперь мы тривиализуем

над

. Что значит тривиализовать расслоение? Это значит установить изоморфизм расслоения

и тривиального расслоения над

со слоем

. Этот изоморфизм даст нам изоморфизм расслоения

и тривиального расслоения над

со слоем

. (Контрольный вопрос: как?) Соответственно мы получим изоморфизм

и

. В последнем случае знаком

я обозначил тривиальное расслоение над

со слоем

; таким образом, я злоупотребляю обозначениями. Возможно, тривиальное раслоение лучше обозначать каким-то другим знаком, но я не могу придумать каким.
Если структурная группа векторного расслоения редуцирована от

к какой-то подгруппе Ли

, а связность согласована с этой

-структурой, то эндоморфизмы слоя

над точкою

, определяемые кривизною, будут не какие попало элементы

, а элементы подпространства

. Значит, кривизна при тривиализации попадёт не просто в

, а в его подрасслоение

. Здесь

-- соответствующая подалгебра Ли.

.

Ну а всё-таки забудем пока про кривизну вообще. Есть алгебра Ли

, она состоит из кососимметрических вещественных

матриц. На ней есть инвариантные многочлены, например определитель: его значение на произвольной матрице

равно

. (Как всегда, имеется в виду инвариантность относительно присоединённого действия

:

для любых

.) Какому инвариантному многочлену соответствует

? Тот же вопрос про

и

и

. Этот вопрос ключевой, подумайте внимательно! Потом надо будет научиться на него отвечать и для случая произвольного ранга.
Комплексификацию я вижу так: берём

, вводим комплексную структуру.
Кажется, сейчас это не самый лучший способ думать про комплексификацию. Что надо сделать, чтобы задать вещественное векторное расслоение ранга

над

? Надо выбрать открытое покрытие

базы

и склеивающий коцикл

из группы

чеховских 1-коцепей, отвечающих покрытию

, с коэффициентами в пучке гладких функций

. Возможно, это звучит страшно; попросту это всё значит, что каждой (упорядоченной) паре открытых множеств

из нашего покрытия

надо сопоставить гладкую функцию

(функцию склейки), причём эти функции должны удовлетворять определённым условиям, чтобы можно было корректно склеить.
(Оффтоп)
На каждом

функция

, на каждом двойном пересечении

функция

, на каждом тройном пересечении

функция

.
Это понятно?
Теперь пусть у нас есть вещественное векторное расслоение, заданное покрытием

и набором гладких функций

Как по нему построить комплексное векторное расслоение, то есть как сделать коцикл со значениями в

? У нас есть замечательное вложение

в

: любую вещественную матрицу можно рассматривать как комплексную. Используя это вложение, мы очевидным образом получаем из набора

-значных функций набор

-значных функций. Это и будет склеивающий коцикл для комплексификации нашего вещественного векторного расслоения.
Операции над векторными расслоениями так и получаются: прямая сумма получается из отображения

, которое пару матриц

переводит в

, комплексно сопряжённое расслоение -- из отображения

, которое комплексно сопрягает матрицы, и так далее: так же получаются двойственные расслоения, тензорные произведения,
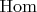
'ы...
Если верно, то не пойму, почему во втором блоке знаки у кривизны меняются. Наверное, из-за комплексной структуры, но каким образом.
Не надо угадывать, надо посидеть и подумать, как из связности там сделать связность тут и что при этом случится с кривизной.