Начнем со следующей гамильтоновой системы

Здесь

гладкая функция

определена в

;
через

обозначена стандартная евклидова норма;

--

-функция. Таким образом, функция Гамильтона

-периодична по

.
То есть по системе стукают молотком через промежутки времени

. Замечательно то, что
если сила, заданная потенциалом  , достаточно велика, то систему швыряет от одного положения равновесия до другого, вдоль любой наперед заданной ломаной, соединяющей эти положения равновесия. Это один из эффектов, который принято ассоциировать с динамическим хаосом.
, достаточно велика, то систему швыряет от одного положения равновесия до другого, вдоль любой наперед заданной ломаной, соединяющей эти положения равновесия. Это один из эффектов, который принято ассоциировать с динамическим хаосом.Перейдем к строгим формулировкам.
Легко показать, что любое решение этой системы представляет собой кусочно постоянную функцию

и непрерывную, кусочно линейную функцию

.
Вводя обозначения

находим
формулы, характеризующие поведение системы на периоде
![$[-\pi,\pi]\ni t$ $[-\pi,\pi]\ni t$](https://dxdy-02.korotkov.co.uk/f/d/a/7/da7028a9ad3fe860d104a34345b7c1c982.png)
:

Откуда

Следовательно, значения

связаны соотношением

Эта формула может быть записана с помощью лагранжиана:

Формула (2) задает отображение

.
При

это отображение является лагранжевой версией отображения Чирикова.
Антиинтегрируемый предел.Рассмотрим следующую дискретную лагранжеву систему:

Через

обозначен малый параметр,

Предположим, что критические точки

(возможно есть и другие критические точки, но мы выбрали это конечное подмножество) функции

невырождены:

Отметим, что каждая из этих точек является положением равновесия дискретной лагранжевой системы (3): последовательность

есть решение рекуррентного соотношения (3).
Через

обозначим множество этих критических точек.
Теорема. Для любого достаточно малого 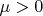 и любой последовательности
и любой последовательности
 существует такое
существует такое  , что для всякого
, что для всякого  найдется решение
найдется решение  дискретной лагранжевой системы (3) такое, что
дискретной лагранжевой системы (3) такое, что
 Схема доказательства.
Схема доказательства. Введем множество

состоящее из последовательностей

таких, что

для всех

. Это множество является полным метрическим пространством относительно метрики

Отображение

является диффеоморфизмом малой окрестности

точки

на малую окрестность нуля

. Причем выберем эти окрестности так, что

Через

обозначим обратный диффеоморфизм,

.
Выберем
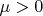
настолько малым, что бы шар

Тогда при достаточно малых

уравнение (3) эквивалентно следующему

В этой системе уравнений

выбрано из условия

.
Система (4) представляет собой задачу о неподвижной точке. Легко показать, что отображение, стоящее в правой части ,при малых

является сжатием пространства

.