Sender, с моим "уровнем" в теории чисел я, предположительно, неспособен доказать не менее 99% даже её известных теорем

Не говоря уже о недоказанных гипотезах, которые и от профессионалов-то ускользают. Я, собственно, заинтересовался этим вопросом для того, чтобы оценить площадь "белых пятен" в моих познаниях. Если их удастся чуть уменьшить - будет уже хорошо.
Экспериментально обнаружилось ещё одно свойство. Берём

- число, делящееся на любое натуральное число до

включительно. Берём

- произведение всех простых чисел, не превосходящих

. Итог выглядит так, словно отношение их логарифмов в пределе на бесконечности равно единице. Вот график отношения логарифмов для

до 100 000:
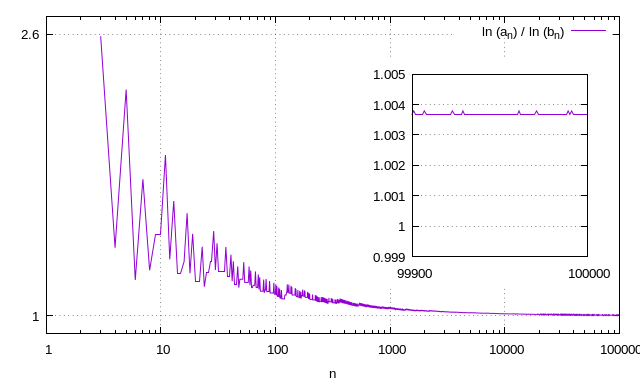
Ниже единицы график опуститься не может никак, поскольку в

имеются все простые числа, и некоторые со степенями. В

те же простые числа, но в степени 1. Физико-интуитивное ощущение такое, словно небольшие составные числа "вынуждены" повторно использовать одни и те же простые числа из-за нехватки строительного материала. Позже, когда выбор расширяется, составные числа в основном образуются из разных простых чисел, взятых по одному разу. Напрашивается связь с энтропией, в которой логарифм - тоже одно из действующих лиц.
Надеюсь на продолжение беседы.