В сети заданы 2 потока

и
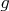
,

. Найдется ли такой путь из

в
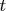
, чтобы для всех вершин

? Найдется ли такая последовательность вершин?
Пыталась придумать контрпример для пути, но так и не вышло, поэтому думаю, что даже путь всегда найдется. Но не очень понимаю как это можно доказать, когда пыталась строить контрпример, всегда есть ребро из источника, на котором значение потока больше, если его пытаться потом разделить, то на одном из ребер оно все равно больше и так строится путь. Но, по логике задачи, в первом случае все же ответ должен быть "нет". Подскажите, пожалуйста, что-нибудь, видимо, я чего-то не понимаю



