то же самое проделать для уравнения

.
Для этого уравнения пытаться доказывать ограниченность решений по

или

не имеет смысла, поскольку они не ограничены. Похоже, что в этой задаче все целочисленные решения не найти; так как есть взаимосвязь с частичной целочисленной факторизации чисел вида

при больших

. Тем не менее некоторые решения (в том числе бесконечные серии) найти можно.
Рассмотрим уравнение относительно

. Так как

имеет тривиальные делители

, проверим можно ли при таких значениях переменной

получить целые

После подстановки получаем:
1.

уравнение

2.

уравнение

3.

, уравнение

4.
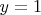
, уравнение

Получаем следующие решения:

, где

любое целое;

, где

любое целое;

,

,

,

;

, где

любое целое;

Рассматриваем теперь уравнение относительно

и поступаем аналогично, находим решение

.
Если положить

, тогда

(появились новые очевидные делители). В результате находятся две новые бесконечные серии решений

,

, где

любое целое.
Эксперимент показывает, что существуют решения, которые определяются нетривиальными делителями

, предположительно таких решений бесконечное множество. Например, если положить

, то решений всего четыре:

Первые два не описываются найденными сериями решений, они связаны с частичной факторизацией

.



