Приведем решение задачи трисекции произвольного угла при помощи циркуля и линейки без делений:
Возьмем произвольный угол
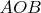
. Построим окружность

с произвольным радиусом и центром в точке

. Построим окружность

с центром в точке

и радиусом

. Обозначим вторую точку пересечения

и

как

. Построим окружность

с центром в точке

и радиусом

. Обозначим вторую точку пересечения

и

как

. Проводим прямую через точки

и

.
По построению угол
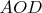
ровно в три раза больше угла
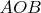
. Поскольку угол
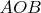
является произвольным, то и угол
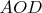
также произвольный. Итак, нам удалось разделить произвольный угол
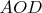
на три равные части при помощи циркуля и линейки без делений.
Подскажите, на что мне лучше всего потратить премию Филдса?