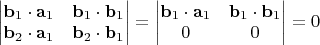Запишем условие ортогональности 2-плоскостей.
Пусть векторы
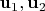
лежат в 2-плоскости

и линейно независимы, а векторы
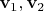
лежат в 2-плоскости

и тоже линейно независимы.
Тогда

и

ортогональны (в «слабом» смысле, как в условии задачи), если
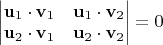
Пусть
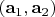
— ортонормированный базис на плоскости

. Для произвольного вектора

длина его ортогональной проекции на плоскость

определяется формулой
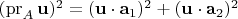
Длина проекции выражена через базисные векторы

, но от выбора базиса не зависит.
Рассмотрим единичный вектор
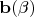
, вращающийся в плоскости

при изменении угла поворота

(относительно некоторого нулевого направления). Выберем значение
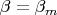
, при котором
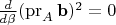
. Обозначая
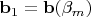
,
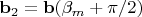
, получим
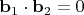
и
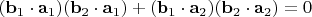
Воспользуемся свободой в выборе базиса в

и потребуем
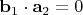
(такой выбор всегда возможен).

Если
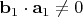
, то обязательно
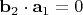
.

Если
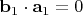
, то
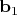
ортогонален любому вектору в

, поэтому
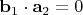
при любом выборе базиса. В этом случае переопределим базис так, чтобы
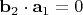
.
Итак, всегда можно считать, что
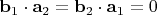
.
Теперь натянем плоскость

на векторы
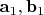
. Проверим, что

ортогональна

:
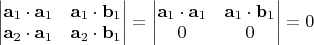
Проверим, что

ортогональна

: