Следует из того, что если

решение уравнения

, то

и

Решений же уравнения

, как доказал Люнггрен, всего два

.
Пара множителей в скобках левой части уравнения

не может быть целыми квадратами, следовательно существует свободное от квадратов

такое, что

. Перепишем это как

, или так

. Сразу нужно заметить, что ситуация эта будет повторяться и для других четных степеней помимо четвертой: двойной Пелль (не взбалтывать!) со степенями в числителях подходящих дробей, в нашем случае с квадратами. Для начала пусть это будут

-е и

-е решения. С первым проблем нет: любое число вида

поделенное на максимально возможный квадрат с большой вероятностью подойдет в качестве

. Например

. Проверяем.

Как видим,

выполняется, но

не является квадратом. Чтобы убедиться в отсутствии квадратов в последующих членах нужно проверять последовательность

.

есть удвоенное

, и это общая закономерность. Поэтому в нашем случае требуется

или

. Решения этого уравнения следуют из разложения
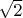
:

и дальше,
как доказал Люнггрен, квадратов в знаменателях нет. Как он это доказал, видимо выходит за рамки школьной программы.

(свободное от квадратов). Именно из разложения

получаем нужное решение. Ну, а если квадрат окажется в числителе

-го решения Пелля?

Видим, что

кратен

и

, откуда

. Что же, в числителях подходящих дробей разложения

не может встретиться двух квадратов? Да нет. Как было не известно, так и осталось. Доказано только, что их не может быть одновременно в

-ом и в

-ом или

-ом решениях за исключением нашего примера. Однако бесконечность количества решений уравнения

оказывается сильно под вопросом, и тем более для четных степеней

. С нечетными не знаю. Где бы почитать об уравнении

или хотя бы один пример увидеть с

-ми степенями?
Что касается отдельной брошюры, то, конечно, эта работа давно делается и в сети имеются сайты этой направленности.
Вижу Вашу поправку. Дайте ссылок пожалуйста, если не затруднит. Именно на "коллекции" целочисленных решений.