Вчера я не имел возможности, а сегодня нарисовал образно, что я имел в виду.
Трёхмерную сферу

(в данном случае единичную сферу вокруг точки

) я представляю себе как "стеклянный шар" (именно шар! заполненный внутри точками!), изображающий развёртку сферы

на плоскость

:
На самом деле, он деформирован (представьте себе развёртку двумерной сферы

на двумерную плоскость

), деформация усиливается к краю, но сейчас я этим пренебрегу. Единственно, надо понимать, что вся "поверхность стеклянного шара" - это одна точка, "внешний полюс", противоположный другой точке - "центральному полюсу". Расстояния внутри "стеклянного шара" - угловые, и расстояние между полюсами - радиус "шара" -

Если вам удобней мыслить в координатах, и хочется как-то сориентироваться по осям, то оси координат пересекают сферу

в таких точках (взят один из вариантов):
(Показаны не все точки, чтобы не загромождать рисунок: в "дальней части стеклянного шара" есть соответствующие точки

а точка
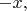
как мы знаем, растянута по "поверхности шара".)
Чтобы немного пообвыкнуться со "стеклянным шаром", проведём через

две прямые и плоскость. Плоскость пересечёт "шар" по экваториальной окружности, то есть не по любой, а с
диаметром 
А прямая пересечёт "шар" в точке, и две показанные прямые - одна лежит в плоскости, а другая - не лежит в плоскости. Отношение перпендикулярности означает "расстояние в шаре"

На самом деле, прямая проходит через шар
в двух точках, отстоящих на расстояние

- такая вторая точка для каждой точки шара единственна, и называется
сопряжённой. Но на этом рисунке я забыл отметить сопряжённые. Точки, сопряжённые экваториальной окружности, лежат на ней же - а для любой другой окружности это неверно.
Теперь проведём через

две произвольные плоскости. Они зададут в шаре две экваториальные окружности общего положения - аналогично скрещенным прямым в 3-мерном пространстве. Для пары точек, взятых на этих окружностях, можно измерить "расстояние в шаре" - по сути, угол между двумя прямыми, проходящими через

(Более строго, два угла, дополняющих друг друга до

) Как и в обычном 3-мерном пространстве, для двух скрещенных прямых существует общий перпендикуляр, проходящий через пару точек с наименьшим расстоянием. Здесь для двух экв. окружностей существует третья экваториальная окружность, проходящая через пару точек с наименьшим расстоянием, и довольно очевидно, что она перпендикулярна каждой из двух данных в точках пересечения (если бы она была не перпендикулярна, то сдвинувшись на небольшое расстояние, мы пришли бы в ещё более близкую точку). Функцию расстояния (точнее, косинус от неё, но косинус монотонен от

до

) я изобразил в предыдущем сообщении.
Если с каждой точкой аккуратно отметить и её сопряжённую, то полный рисунок станет таким. Общий перпендикуляр не может "промахнуться" мимо 3-й и 4-й точки, потому что они сопряжены по своим соответствующим окружностям 1-й и 2-й точке. Здесь видно, что одна и та же прямая (общий перпендикуляр) отвечает как наименьшему расстоянию для пары точек, так и наибольшему - если для одной из точек перейти к сопряжённой.
Теперь немного повернём 3-сферу

возьмём немного другую проекцию в "стеклянный шар" - такую, чтобы первая из окружностей распрямилась в прямую, проходящую через центр и стенки "шара". Тогда рисунок станет вот таким (общий перпендикуляр я наметил пунктиром, чтобы не загромождать рисунок):
Теперь стало легче разглядеть второе решение - общий перпендикуляр, соответствующий не максимумам и минимумам, а седловым точкам (см. предыдущее сообщение):
Всё это я нарисовал не то чтобы для данной задачи, а на будущее, чтобы у автора темы появился инструмент рассуждений о 4-мерном пространстве.
Для
george66 замечание: те же образы используются для пространства

(возникающего много где, например, для эллиптического пространства, для пространства группы

), достаточно только взять в "стеклянном шаре" его внутреннюю половину, отстоящую от "центрального полюса" на расстояние не больше

Тогда из каждой пары сопряжённых точек выживает только одна.
Для всех: в таком "шаре" легко строить двойственные конструкции и теоремы, которые получаются одна из другой заменой
прямая  3-мерное пространство;
3-мерное пространство;
плоскость  двойственная ей (дважды перпендикулярная) плоскость.
двойственная ей (дважды перпендикулярная) плоскость.



