DFS на дополненном графе

[Darts501]

Дан граф $G = (V, E)$, тогда дополненным графом графа $G$ называется граф $G'=(V', E')$, в котором $V = V'$ , $E \cap E' = \varnothing$, $E \cup E' = $ множество ребер полного графа на вершинах $V$. Нужно осуществить $DFS$ (поиск в глубину) на графе $G'$, зная граф $G$, $n = |V|, m = |E|$.

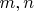
Проблема в том, что $m, n$ порядка $10^5$, тогда $|E'|$ порядка $10^{10}$. Поэтому явно найти ребра $E'$ нельзя. Но для любых двух вершин $v, u$ можно за $\log m$ узнать есть между ними ребро или нет, например положив ребра в $set$. Теперь можно осуществить поиск в глубину следующим образом. Начинаем с некоторой вершины, например 1, остальные помечаем как не посещенные. Пусть мы щас находимся в вершине $v$. Просматриваем не посещенные вершины, если есть ребро из текущей вершины в $v$ (т.е. в графе $G$ нет такого ребра) тогда переходим в текущую, если нет, то пропускаем.
Этот алгоритм осуществляет поиск в глубину. Но я не вижу способа как его реализовать быстрее чем $O(n k \log m)$, где $k$ - количество вершин, в которые можно попасть из стартовой в графе $G'$. Вроде бы можно с таким порядком $O((n + m)\log m)$. Не могу придумать как. Гугление ничего не дало.
Скажите как можно это сделать или где об этом можно почитать.

[mihaild]

Да можно как вы пишете: находясь в вершине, перебираем все непосещенные, пока не найдем, в какую можно пойти (только тут когда мы вернемся в эту вершину нужно аккуратно продолжить перебор с того места, на котором остановились, а не начинать заново). В итоге в каждом вызове DFS у нас будет цикл по еще непосещенным вершинам, и в нем будет два вида итераций: на которых мы заходим дальше (потому что ребра до этой вершины в $G$ не было) и на которых не заходим (потому что ребро было). Оцените количество итераций каждого вида.
А если еще и ребра сложить хранить в более подходящей структуре, то вообще за линейное время всё сделать можно.

(Заголовок)

ИМХО лучше было бы сказать "на дополнении графа" вместо "на дополенном графе"

[Darts501]

Пусть в $G'$ есть ребра из вершины 1 во все вершины $2, \ldots , k$ и больше нет. В вершине 1 нужно просмотреть вершины $2, \ldots, n$. Заходим в вершину 2, нужно просмотреть $3,\ldots, n$ и когда мы находимся в вершине $i \forall i = 1,\ldots, k$ нужно смотреть вершины $i + 1, \ldots, n$. Каждый просмотр требует $O(\log m)$ времени. В итоге получаем асимптотику $O(n k \log m)$. Мы не может просматривать не посещенные вершины одним циклом, для каждой новой вершины просмотр нужно начинать с начала.
Я конечно что то не понимаю, но что?)) Объяснений пока не достаточно

А насчет того, чтобы избавиться от логарифма, подходящая структура данных это совершенное хеширование(ведь множество ребер не меняется)? какие еще могут быть варианты?

[mihaild]

Darts501 в сообщении #1381705 писал(а):

Заходим в вершину 2, нужно просмотреть $3,\ldots, n$

Не перескакивайте. Вот мы зашли в вершину $2$. Куда дальше пошли?
После того как закончили со следующей вершиной и вернулись в $2$ - какие у нас остались вершины? Какие вершины нам нужно еще раз проверить?

[Geen]

Прошу прощения что встреваю, но в чём практический смысл этой задачи?

[Darts501]

В вершине 2 посмотрел список от 3 до $n$, никуда не смог попасть. Возвращаюсь в вершину 1, там продолжаю просматривать список с вершины 3. Иду в 3, там смотрю от 4 до $n$, никуда не могу попасть, возвращаюсь в 1, продолжаю смотреть с 4 вершины. Из списка не посещенных удаляем только, если можем пройти в эту вершину и из этой вершины вызываем дфс. Для каждой вершины из которой вызван дфс, нам нужно просматривать текущий список не посещенных сначала, информация о там что какая то вершина из списка была просмотрена из других вершин и не была из него выброшена ничего нам не дает, сможем ли попасть в эту вершину или нет. Как избавится от квадрата?

даже если вначале для 1 вершины проходим список от 2 до $n$ и все вершины, в которые мы можем попасть, удаляем из списка не посещенных и добавляем в дополнительный список. Потом запускаем дфс из каждого элемента доп списка, то все равно сложность такой же будет.

Geen в сообщении #1381725 писал(а):

Прошу прощения что встреваю, но в чём практический смысл этой задачи?

У меня интерес чисто алгоритмический. А вообще граф же $G'$ частный случай неявного графа. Например задача решения кубика-рубика. Если некоторое положение это вершина, а ребро соединяет две вершины если за одно движение можно попасть в другую. Тогда задача собрать кубик - это найти путь в таком графе. Понятно что нельзя такой граф представить в памяти компьютера. Есть начальная вершина и некоторые правила, по которым мы можем строить новые ребра. Вот чисто практическая задача))

[mihaild]

А, я не посмотрел что у вас в $G^\prime$ мало ребер, а не в самом $G$. Ну тогда в исходном $G$ ребер много (квадрат по числу вершин), а алгоритм отработает как раз за линейное от числа ребер время.
Быстрее чем за число ребер в $G$ и не получится.