Размножение и статистика

[vpb]

Привожу свое решение, со всеми подробностями.

Пусть $N$ есть общее число семей. Из них $N/3$ относятся к каждому из типов $A$, $B$ и $C$ соответственно.

Будем считать, что семьи каждого из типов образуются (и исчезают) с постоянной скоростью, скажем $v_A$ семей типа $A$ в единицу времени. Заметим, что семьи типа $A$, существующие в момент времени $t$ --- это в точности те, которые возникли в промежутке $[t-3, t]$. Следовательно, $v_A(t-(t-3))=N/3$, $3v_A=N/3$, $v_A=N/9$. Точно так же $v_B=v_C=N/9$. Будем обозначать $v_A=v_B=v_C=N/9$ дальше просто через $v$.

Пусть $n_{A,1}$ --- число семей типа $A$, родивших первого ребенка в промежуток времени $[t, t+dt]$. Аналогичным образом определим числа $n_{A,2}, \ldots, n_{C,3}$. Отметим, что $n_{A,2}=n_{A,3}=n_{B,3}=0$.

То, что семья типа $A$ родила ребенка в промежуток $[t, t+dt]$, означает, что она образовалась в промежуток времени $[t-1/3, t-1/3+dt]$. Таких семей $v\,dt$. Итак, $n_{A,1}=v\,dt$. Аналогично $n_{B,1}=\ldots=n_{C,3}=v\,dt$.

Семьи, родившие ребенкав промежутке $[t, t+dt]$, доход которых находится в диапазоне $I=[0.5, 1.5]$ --- это в точности семьи, родившие первого ребенка. Их число есть $n_I=n_{A,1}+n_{B,1}+n_{C,1}= 3v\,dt=(N/3)\,dt$. Аналогично, число семей, родивших ребенка в этом промежутке времени, доход которых находится в диапазоне $II=(1.5, 2.5]$ --- это $n_{II}=n_{B,2}+n_{C,2}=2v\,dt=(2/9)N\,dt$. Наконец, семей, родивщих ребенка и находящихся в диапазоне $III=(2.5, 3.5]$, есть $n_{III}=v\,dt=(N/9)\,dt$.

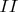
Теперь фиксируем какой-то момент времени $u$ и найдем число семей, которые в этот момент находятся по доходу в одном из диапазонов $I$, $II$, $III$. Обозначим соответствующие числа $M_I$, $M_{II}$, $M_{III}$. Ясно, что

$$ M_I=M_{I,A}+M_{I,B}+M_{I,C}\,, \qquad M_{II}=M_{II,A}+M_{II,B}+M_{II,C}\,,$$

$$ M_{III}=M_{III,A}+M_{III,B}+M_{III,C}. $$

Здесь $M_{I,A}$ есть число семей, принадлежащих к типу $A$, доход которых лежит в $I$, и т.д.

Ясно, что $M_{I,A}=N/3$, $M_{II,A}=M_{III,A}=M_{III,B}=0$. Семья типа $B$ имеет доход в диапазоне $I$ в том случае, если она образовалась в промежутке $[u-1/3, u]$. Таких семей есть $(1/3)v=N/27$. Аналогично $M_{I,C}=M_{II,C}=N/27$. Отсюда $M_{II,B}=N/3-M_{I,B}=N/3-N/27=(8/27)N$, а также $M_{III,C}=N/3-M_{I,C}-M_{II,C}=N/3-2\cdot N/27=(7/27)N$.
Складывая, находим $M_I=N/3+N/27+N/27=(11/27)N$, $M_{II}=(8/27)N+N/27=N/3$, $M_{III}=(7/27)N$.

Вероятность $p_1$, о которой говорится в условии --- это $n_I/M_I=(N/3)\,dt/(11/27)N=(9/11)\,dt$.
Также $p_2=n_{II}/M_{II}=(2/9)N\,dt/(N/3)=(2/3)dt$, $p_3=n_{III}/M_{III}=(N/9)\,dt/(7/27)N=(3/7)dt$.

Значит, $p_1 : p_2 : p_3= 9/11 : 2/3 : 3/7 =3/11 : 2/9 : 1/7 = 189 : 154 : 99$.

-- 27.02.2019, 04:06 --

Заметим, ответ такой же, как у Geen. Коллега EUgeneUS не туда посчитал единичку (что называется, дело житейское ): надо $23$ заменить на $22$, а $17$ на $18$, и получится то же самое. В общем, вычисление произведено и проверено. Спасибо участвовавшим.

[пианист]

EUgeneUS в сообщении #1378493 писал(а):

Если мы будем выбрать случайно детей, а потом смотреть, какой доход был у родителей (1, 2 или 3) на момент рождения, то будет такое отношение вероятностей.

Да, я представлял себе что-то типа опроса в роддоме