Алексей, спасибо что продолжаете попытки усовершенствовать алгоритм.
Я написал функцию возвращающую центр дуги и тестирую ее. Пока что удается ее завалить.
Суть этой функции в этом уравнении

обозначим это уравнение - (!!)
вот код, реализующий это уравнение:
Код:
a2 = a*a; b2 = b*b; A = x/a2; B = y/b2;
C = (1/a2 - 1/b2)*x.*y;
D = -(x.*x/a2 + y.*y/b2 - 1)/2;
M = [A B C D]; X = pere_slau(M);
Mo.X = -X(1); Mo.Y = -X(2); fi = X(3);
Т.е. аппроксимация ведется (пока) по всем точкам дуги и нахожу ее центр Мо и угол наклона fi.
Затем получаю матрицу поворота и переноса
Код:
Mper = [1 0 -Mo.X; 0 1 -Mo.Y; 0 0 1];
s = sin(fi); c = cos(fi);
Mpov = [c s 0; -s c 0; 0 0 1];
MT = Mpov*Mper;
Затем с ее (МТ) помощью переношу все точки дуги и повторяю процедуру нахождения Мо и fi. Это совсем краткое описание (могу это развернуть и подробно по шагам описать)
Главное вывод: любую (с некоторыми пока до конца не ясными ограничениями) дугу можно аппроксимировать эллипсом с произвольно заданными длинами осей. Уравнение (!!) дает такую возможность (должно дать). Полученный результат дает примерно то же самое как и аппроксимация набора точек на плоскости окружностью
(Оффтоп)
Код:
function [Mo R] = approx_circle(x, y)
N = length(x); k = 1/N; k2 = 2*k;
sumx = sum(x); sumy = sum(y);
x2 = x.*x; x3 = x.*x2; sumx2 = sum(x2); sumx3 = sum(x3);
y2 = y.*y; y3 = y.*y2; sumy2 = sum(y2); sumy3 = sum(y3);
sumxy = sum(x.*y);
sumx2y2 = sum(x2+y2);
sumxy2 = sum(x.*y2);
sumx2y = sum(x2.*y);
sumX = sumx2y2*sumx;
sumY = sumx2y2*sumy;
a1 = k2*sumx*sumx - 2*sumx2;
b1 = k2*sumx*sumy - 2*sumxy;
b2 = k2*sumy*sumy - 2*sumy2;
c1 = sumx3 + sumxy2 - k*sumX;
c2 = sumy3 + sumx2y - k*sumY;
xo = (b1*c2 - c1*b2)/(a1*b2 - b1*b1);
yo = (b1*c1 - a1*c2)/(a1*b2 - b1*b1); Mo.X = xo; Mo.Y = yo;
R = sqrt(xo*xo + yo*yo + k*sumx2y2 - k2*(xo*sumx + yo*sumy));
end
эта ф-ция работает всегда, важно только чтобы точки не лежали на одной прямой и чтобы точек было больше двух. Надежность в этом деле самое главное. По ходу тестирования у меня возникает масса трудностей. Раз вы еще здесь, то поделюсь ими.
На самом деле ур-е (!!) применяется не к исходным координатам дуги, а к уже перенесенным за счет нулевого приближения. Это большой недостаток этого метода, т.к. не всегда просто найди это нулевое приближение. Может быть возможно было бы в самое исходное ур-е эллипса подставить скажем не

тоже самое с

и с

, т.е. вместо

подставить

и получим не это:

а нечто гораздо сложнее. Но может быть его можно упростить за счет отбрасывания малых членов

Если бы это удалось сделать, то тогда бы нулевое приближение было бы не нужным! Но пришлось бы с самого начала находить

Впрочем может быть это мои иллюзии ибо как можно с самого начала отделить

и
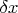
и т.д. ?



