Консервативная схема для решения дифференциального уравнения

[qwertynosik]

Добрый день. Разбирался с различными схемами решения квазилинейных дифференциальных уравнений в частных производных и возник вопрос касательно применимости консервативных схем. Я разбираюсь с применением разностных схем на примере уравнения Хопфа:
$u_t+uu_x=0$
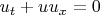
Либо, если его записать дивергентной форме:
$u_t+\frac{(u^2)_x}2=0$
Пусть мы рассматриваем уравнение на отрезке $x\in(X_0, X_1)$ по координате и на отрезке $t\in(0, T)$ по времени и имеем "хорошее" начальное условие без разрывов, скажем $u(x, 0)=e^{-\frac{x^2}2}$.
Если проинтегрировать это уравнение по координате и по времени в этих пределах, получим закон сохранения:
$\int_{X_0}^{X_1}dx(u(x, T)-u(x, 0)) + \frac12 \int_{0}^{T}dt((u(x_1, t))^2-(u(x_0, t))^2) = 0$

Теперь построим разностную схему для решения уравнения в дивергентной форме на сетке $x_n=X_0+nh$, $n\in[0, N]$, $t_m=m\tau$, $m\in[0, M]$:
$\frac{u^{m+1}_n-u^{m}_n}\tau+\frac{(u^{m}_{n+1})^2-(u^{m}_n)^2}{2h}=0$
Верхний индекс $u$ обозначает слой по времени, нижний индекс - по координате.
Теперь попробуем просуммировать данное выражение по всей сетки, аналогично интегрированию уравнения:
$\sum_{0}^{N-1}\sum_{0}^{M-1}h(u^{m+1}_n-u^{m}_n) + \frac12 \sum_{0}^{M-1}\sum_{0}^{N-1}\tau({(u^{m}_{n+1})^2-(u^{m}_n)^2}) = 0$
Преобразуем суммы:
$\sum_{0}^{M-1}(u^{m+1}_n-u^{m}_n) = u^M_n-u^0_n$
$\sum_{0}^{N-1}({(u^{m}_{n+1})^2-(u^{m}_n)^2}) = (u^m_N)^2-(u^m_0)^2$
Тогда получим:
$\sum_{0}^{N-1}h(u^M_n-u^0_n) + \frac12 \sum_{0}^{M-1}\tau({(u^m_N)^2-(u^m_0)^2}) = 0$
Тут видно, что в пределе, когда разбиения сетки стремятся к нулю, то есть $h\rightarrow0$ и $\tau\rightarrow0$, то данные суммы стремятся к интегралу, по сути мы считаем интеграл методом прямоугольников, который как известно имеет ошибку порядка h:
$\sum_{0}^{N-1}h(u^M_n-u^0_n)=\int_{X_0}^{X_1}dx(u^M(x)-u^0(x)) + R(h)$
$\sum_{0}^{M-1}\tau({(u^m_N)^2-(u^m_0)^2})=\int_{0}^{T}dt({(u_N(t))^2-(u_0(t))^2}) + R(\tau)$
Тогда закон сохранения, общем случае, выполняется не абсолютно точно:
$\sum_{0}^{N-1}\sum_{0}^{M-1}h(u^{m+1}_n-u^{m}_n) + \frac12 \sum_{0}^{M-1}\sum_{0}^{N-1}\tau({(u^{m}_{n+1})^2-(u^{m}_n)^2}) = R(\tau)+R(h) $
То есть мы получили, что в консервативной схеме, которая должна сохранять некоторую величину, это величина (в данном случае энергия), сохраняется с некоторой ошибкой, пропорциональной шагу сетки.
Но проделав аналогичные выкладки с недивергентной формой записи уравнения Хопфа, получим 3 члена, а не 2, и ошибка опять будет пропорциональна шагу сетки. В связи с чем возникает вопрос - либо оценка проведена неправильно, и где то есть ошибка, так что на самом деле консервативная схема дает сходимость более высокого порядка, либо же, если все верно, то в чем принципиальная полезность консервативной схемы? Обе схемы дают одинаковую сходимость, ошибки соизмеримые по величине (При расчете по данной схеме я получил, что ошибка неконсервативной схемы сего в 2-3 раза больше, чем консервативной). Зачем нужна консервативная схема?

[Pphantom]

А откуда следует, что рассматриваемая схема является консервативной? Того, что она получена разностной аппроксимацией уравнений в дивергентной форме, для консервативности недостаточно.

P.S. Необходимым условием консервативности дивергентная форма уравнений, кстати, тоже не является.

[qwertynosik]

Pphantom в сообщении #1363847 писал(а):

А откуда следует, что рассматриваемая схема является консервативной? Того, что она получена разностной аппроксимацией уравнений в дивергентной форме, для консервативности недостаточно.

P.S. Необходимым условием консервативности дивергентная форма уравнений, кстати, тоже не является.

Ну данная схема все таки сохраняет величину $\int_{X_0}^{X_1}dx(u(x, T)-u(x, 0)) + \frac12 \int_{0}^{T}dt((u(x_1, t))^2-(u(x_0, t))^2)=0$ с точностью $R(h)+R(\tau)$. А схема для уравнения в недивергентной форме будет сохранять эту величину с точностью до $h\frac12\int|u_x|^2dxdt$, так что если будет иметь место разрыв, то производная $u_x$ будет таки не ограничена и сохранения, все таки, не будет. В моем понимании так.

[Pphantom]

Так ведь схема будет консервативной, если для интегральных соотношений (т.е. обобщенных решений) она будет выглядеть так же. У вас это есть?