Теперь мы изложенное выше обобщим и улучшим.
Пусть

. Разобьем отрезок

на

частей

, где
![$I_t=[(t-1)/s; t/s]$ $I_t=[(t-1)/s; t/s]$](https://dxdy-02.korotkov.co.uk/f/9/4/b/94b16874d6599a30fecc31c84a4e37a982.png)
. Определим

Также определим функции


короче,

где

при

,

при

,

при

.
Аналогично положим

Сумму для

разобьем на два слагаемых:

, где

--- сумма всех слагаемых, отвечающих тем парам

, для которых

и

лежат в разных отрезках

, а

--- тем парам, дляя которых они лежат в одном

. Понятно, что если значения

и

распределены по отрезку

примерно равномерно, то во вторую сумму попадает примерно

-я доля всех слагаемых, а все остальные (т.е. почти все, при

) --- в первую.
Сумму

вычисляем непосредственно.
Затем рассмотрим вычисление суммы

. Для

пусть

--- номер того из отрезков

, в который попадает

. Аналогично определим

тем, что

.
Выпишем формулу для

(обдумать и проверить ее правильность оставляю Вам самому):

Применение этой формулы даже для небольших

дает выигрыш в скорости вычисления функции

.
Теперь рассмотрим вопрос о том, каковы вычислительные ресурсы (время и память), нужные для вычисления

. Мы покажем, что время, по существу, примерно то же, что и при вычислении по (неверной) формуле

а памяти надо в

раз больше.
Для простоты оценок будем считать, что

.
Пусть

--- число узлов сетки, в которых табулируются

и

. При вычислении по старой формуле табуляция функций

и

требует, очевидно,

арифметических операций (вычисление каждого слагаемого

требует, очевидно, не более

арифметических операций, где

--- некоторая не очень большая постоянная (порядка нескольких десятков).) Объем же памяти для хранения значений

и

есть

, очевидно (надо хранить значения

и

во всех узлах).
При вычислении "по новому" памяти надо в

раз больше, так как нам надо хранить значения в тех же узлах

функций

,

.
Собственно вычисление распадается на две части:
(1) табулирование значений функций

,

и
(2) применение найденной таблицы к вычислению функции

.
(Есть еще (2а) --- вычисление части

, которая рассматривается несколько позже.)
Часть (2) имеет ту же трудоемкость, что и в "неправильной" ситуации (это ясно, более-менее).
Для вычисления значений функций

в узлах мы вычисляем те же самые слагаемые

, что и раньше. Однако, теперь эти слагаемые дают вклады в
разные функции
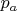
. Но всего слагаемых столько же, сколько и ранее, а именно порядка

. А стало быть, и сложность
та же. После того, как вычислены все числа

, мы вычисляем все

. При этом, заметим, не обязательно каждый раз (для каждого

) вычислять сумму из

слагаемого. Мы можем вычислить

, это требует

операций, а затем вычислить

последовательно, используя соотношение

. Это опять потребует

операций. Таким образом, общая сложность табулирования функций

и

есть

. Что касается вычисления слагаемых

, то оно для каждого

имеет сложность порядка

операций.
(Изложенное рекомендуется продумать и проверить. У меня, знаете ли, тоже бывают ошибки.)



