Sonic86 писал(а):
Уравнение

аналогично уравнению Пелля.
Осмелюсь утверждать, что решается оно аналогично.
То есть если

- наименьшие по абсолютной величине числа такие, что

,
Прежде всего, если такие

существуют (а ведь могут и не существовать).
Кроме того, вы решаете другое уравнение:

которое получается из исходного только при четном

. Причем


и

Sonic86 писал(а):
то все его решения

находятся из

. При это

нечетно, чтобы

.
Выражая

через

получаем, что
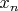
делится на
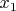
, а

делится на

. Если потребовать, чтобы

были простыми,
то необходимо, чтобы

, откуда

, а

- числа Фибоначчи.
Значение
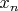
не является в точности значением

или

в исходном уравнении, а поэтому вывод о том, что

неверен.
Кроме того, даже если бы это было так, то получается

(а не

), но это значение не соответствует никакому исходному

.
Sonic86 писал(а):
А уравнение вроде разрешимо
Погадаем на кофейной гуще?

"Вроде" - не аргумент.