george66
А известны простые примеры конкретных не иррациональных чисел, рациональность которых вывести притом нельзя?
Не приходит на ум. Но в интуиционистской математике вообще всё делают по-другому. Главный объект изучения - не множество действительных чисел, а упорядоченное множество (полная решётка) открытых подмножеств

. Для неё можно дать независимую простую аксиоматику, поскольку любое открытое множество есть объединение интервалов с рациональными концами. Непрерывные функции из

в

изображаются "правильными" отображениями этой решётки в себя (соответствуют взятию прообраза, прообраз открытого множества относительно непрерывной функции открыт)
http://www.cs.man.ac.uk/~hsimmons/FRAMES/frames.html-- 26.11.2018, 15:28 --Иррациональное число так и определяется (как действительное, не являющееся рациональным)
Тогда вопрос в том, можно ли сведение некоторого утверждения к абсурду считать доказательством отрицания этого утверждения.
Someone в одной старой теме утверждал, что нельзя. Если так, то обсуждаемое доказательство всё-таки неконструктивно.
Можно (правило приведения к абсурду). Его часто путают с доказательством от противного, когда мы предполагаем
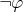
, выводим противоречие и заключаем, что верно

(по правилу приведения к абсурду мы получаем только

)