ЛинАл: принадлежность к линейной оболочке

[logunov]

Здравствуйте, уважаемые члены форума. Большое спасибо за внимание, проявленное к заголовку, излагаю проблему, подход, вопросы.

Проблема:
Пусть $F$ - линейное отображение: $R^3 \to R^4$, такое, что:
$(1,0,0) \overrightarrow{F} (1,1,1,1)$
$(0,1,0) \overrightarrow{F} (0,1,0,0)$
$(0,0,1) \overrightarrow{F} (0,1,a,0)$
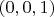
При каком действительном значении параметра $a$ вектор $(0,0,1)$ принадлежит линейной оболочке векторов

Подход:
Линейная оболочка векторов - это число векторов, образующих базисный минор получившейся матрицы из вектор-строк, записанных столбцами, при этом размерность линейной оболочки равна числу базисных векторов полученной матрицы. $(1,0,0) \overrightarrow{F} (1,1,1,1)$
$(0,1,0) \overrightarrow{F} (0,1,0,0)$.
То есть, кажется, что верным было бы поступить следующим образом:
1) Записать $(1,1,1,1)$, $(0,1,0,0)$,$(0,1,a,0)$ в виде матрицы:

$$\begin{pmatrix} 1 \qquad 0 \qquad 0\\ 1 \qquad 1 \qquad 1\\ 1 \qquad 0 \qquad a \\ 1 \qquad 0 \qquad 0 \end{pmatrix}$$

Которая элементарными преобразования переходит к виду:

$$\begin{pmatrix} 1 \qquad 0 \qquad 0\\ 0 \qquad 1 \qquad 1\\ 0 \qquad 0 \qquad a \\ 0 \qquad 0 \qquad 0 \end{pmatrix}$$

(вычел из каждой строки первую по разу)
Ранг матрицы равен трём, а базисные векторы таковы:
$(1,0,0,0)$
$(0,1,0,0)$
$(0,1,a,0)$

Вопросы (они же попытки решения задачи):
1) Кажется, что можно опустить у каждого вектора нулевое значение, т.е записать их в виде:
$(1,0,0) $, $(0,1,0)$, $(0,1,a)$, верно ли это? Если нет, то о чём нужно подумать, чтобы понять почему?
2) Я не совсем понимаю, почему нужно записывать векторы столбцами, а не строками, плюс, когда я вычитаю строки, я... Вычитаю координаты вектора из самого себя? Но это же меняет сам вектор, я прав? Дело в том, что правило о вычитании я нашёл в очень странном месте, а как найти линейную оболочку я не очень представляю, поэтому пробую.
3) Верен ли мой подход к решению? Я не совсем понимаю, как связаны между собой линейная оболочка и параметр: ведь линейная оболочка - это множество линейно независимых векторов, определяющих пространство, которое их комбинации могут занять. Соответственно, кажется, что для принадлежности оболочки, третий вектор должен быть линейно зависимым, то есть, представляться комбинациями остальных линейно зависимых векторов, но так ли это на самом деле?
4) Не совсем понимаю, зачем здесь даётся отображение, кажется, что линейный оператор ни на что не повлияет, так как параметр находится в результате действия оператора, а спрашивается принадлежность к оболочке от векторов, к которым применён оператор. Возможно, я что-то упускаю, но что именно?
5) Нигде не могу найти похожих задач, можете ли посоветовать задачник, в котором есть подобные примеры, если есть возможность, то с решениями?


Большое спасибо за проявленное внимание. Выражаю свою благодарность за уделённое время.

[alcoholist]

logunov в сообщении #1351303 писал(а):

При каком действительном значении параметра $a$ вектор $(0,0,1)$ принадлежит линейной оболочке векторов

Каких именно векторов?

-- Сб ноя 03, 2018 08:48:19 --

logunov в сообщении #1351303 писал(а):

Которая элементарными преобразования переходит к виду

Каков смысл элементарных преобразований матрицы оператора?

[logunov]

Прошу прощения, от усталости показалось, что я их указал.

"Принадлежит линейной оболочке векторов $F(1,0,0)$ и $F(0,1,0)$".
Как я понял, эта запись означает, что к векторам $(1,0,0)$ и $(0,1,0)$ применён линейный оператор $F$.

[alcoholist]

logunov в сообщении #1351303 писал(а):

Кажется, что можно опустить у каждого вектора нулевое значение

У векторов нет никаких значений!

logunov в сообщении #1351303 писал(а):

Я не совсем понимаю, почему нужно записывать векторы столбцами, а не строками

Есть вектора-столбцы и вектора-строки, тут главное понимать, с чем имеете дело в каждой конкретной ситуации.

[Someone]

logunov в сообщении #1351303 писал(а):

Линейная оболочка векторов - это число векторов

Ни в коем случае не число. Проверьте по учебнику.

logunov в сообщении #1351303 писал(а):

образующих базисный минор получившейся матрицы из вектор-строк

Неверно. Проверьте по учебнику.

logunov в сообщении #1351303 писал(а):

Пусть $F$ - линейное отображение: $R^3 \to R^4$, такое, что:
$(1,0,0) \overrightarrow{F} (1,1,1,1)$
$(0,1,0) \overrightarrow{F} (0,1,0,0)$
$(0,0,1) \overrightarrow{F} (0,1,a,0)$

Обозначения какие-то уж очень экзотические. Сами придумали?

logunov в сообщении #1351303 писал(а):

При каком действительном значении параметра $a$ вектор $(0,0,1)$ принадлежит линейной оболочке векторов

Я думаю, что надо начать с определения линейной оболочки и с характеристики векторов, принадлежащих линейной оболочке.

[Munin]

Someone в сообщении #1351386 писал(а):

Обозначения какие-то уж очень экзотические. Сами придумали?

Я подозреваю, это попытка изобразить

$(1,0,0) \shortmid\joinrel\xrightarrow{F} (1,1,1,1)$
$(0,1,0) \shortmid\joinrel\xrightarrow{F} (0,1,0,0)$
$(0,0,1) \shortmid\joinrel\xrightarrow{F} (0,1,a,0)$

Кстати, почему-то \xrightarrow отсутствует в теме "FAQ по тегу [math]".

[bot]

alcoholist в сообщении #1351308 писал(а):

logunov в сообщении #1351303

писал(а):
При каком действительном значении параметра $a$ вектор $(0,0,1)$ принадлежит линейной оболочке векторов

Каких именно векторов?

logunov в сообщении #1351309 писал(а):

Принадлежит линейной оболочке векторов $F(1,0,0)$ и $F(0,1,0)$

Вектор $(0,0,1)$ лежит в $\mathbb R^3$, а $F(1,0,0)$ и $F(0,1,0)$ - в $\mathbb R^4$

[Ruslan_Sharipov]

Примерно 3.5 года назад подобная задача обсуждалась в другом месте: eek.diary.ru. Там она грамотно сформулирована.

Примечание. Не люблю когда вектор записывают в строчку. Вектор, записанный в строчку, - это ковектор. Авторы многих учебников не делают различий и вообще не касаются темы сопряжённого пространства. Эта небрежность передаётся из поколения в поколение. Линейная алгебра - простая наука. Однако она требует аккуратности формулировок и должна такую аккуратность воспитывать. Затем эта аккуратность будет полезна для понимания более сложных наук.

[ewert]

Ruslan_Sharipov в сообщении #1351602 писал(а):

Вектор, записанный в строчку, - это ковектор. Авторы многих учебников не делают различий и вообще не касаются темы сопряжённого пространства. Эта небрежность передаётся из поколения в поколение.

Это не небрежность. Строчки ровно так же векторы, как и столбцы. Только в сопряжённом пространстве. Но только тогда, когда до введения сопряжённого пространства дело вообще доходит. А необходимость доходить возникает далеко не всегда. И до тех пор, пока не дойдёт -- необходимо чётко осознавать, что ковекторы (даже если мы не знаем, что это такое) суть не что иное, как тоже векторы.

И, кстати: многие извращенцы маркоцеписты предпочитают под векторами понимать именно строки. И умножать их на матрицу, соотв., справа. И ничего -- прекрасно себя чувствуют.

[Ruslan_Sharipov]

ewert в сообщении #1351728 писал(а):

Это не небрежность.

Ну как же не небрежность? Если до сопряжённого пространства дело не дошло, если координаты вектора выписаны в строчку, и если на матрицу они умножаются справа, то композиции линейных отображений будет соответствовать перевёрнутое произведение их матриц. Или же аргументы отображений (функций) им придётся писать слева от значков функций. Такому извращенству в обычной жизни нет оправданий.