Цитата:
Вас пугает кубическое уравнение?
Пугает не задачка, а усложнения, возникающие при ее решении. Вот если, например, решать ее по методу Кардано (сделал выкладки решения вчера ночью), то в итоге получается нехилая формула, причем, что особенно неприятно, необходимо делать сравнение дискриминантов

и

, что покажет количество корней и их тип (действ./компл.)!
Цитата:
и ищете этот корешок сколь угодно точными приближёнными методами.
Это дополнительные затраты времени. А значение координаты Y на кривой Безье мне нужно будет определить не один раз, а многократно, т.к. вычисление координат точки на кривой Безье предполагается использовать в составе итерационной процедуры оптимизации, следовательно, приближенные методы определения координат сильно затормозят работу всего алгоритма в целом!
Я тут на досуге рассудил (но еще не успел проверить) следующим образом. Если известно, что параметр

в уравнениях параметрической кривой отвечает за пропорциональное положение (в долях от нуля до единицы) точек вычисления соответствующих значений

параметрической кривой, то не лучше ли будет
сразу найти такое значение

, лежащее в интервале
![$t\in[0,1]$ $t\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/8/9/489dfef0eefc2611fce620116590ce8982.png)
, которое точно будет соответствовать положению заданной абсциссы

(для которой требуется вычислить значение

) - об этом Вы уже говорили выше, но предлагали для этого решить кубическое уравнение

.
Мне подумалось, что определение значения

, совпадающего с положением абсциссы

можно осуществить исходя из пропорции:

,
где

и

- соответственно начало и конец интервала (сегмента), на котором построена кривая (элементарная).
Таким образом, если

совпадет с началом сегмента, то значение параметра
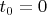
, а если

совпадет с концом сегмента, то параметр

. Любое другое возможное значение абсциссы

НА ДАННОМ ИНТЕРВАЛЕ(!) будет иметь соответствующее значение

,
![$t_0\in[0,1]$ $t_0\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/a/4/ca469642375915eb0455acb0ac31d21e82.png)
, пропорциональное длине интервала. В этом случае, получив величину

найдем

.
Конечно же, перед вычислением значения

, необходимо будет очевидным способом определить, а на какой же именно сегмент составной кривой приходится значение заданной абсциссы

, иначе мы ошибочно попадем на "чужой" интервал (сегмент составной кривой) и, соответственно, на "чужие" параметрические уравнения соседнего сегмента.
Таким мне видится решение. Каково Ваше мнение?