На странице сто в учебнике "Обыкновенные дифференциальные уравнения" В.И. Арнольда есть такое замечание:
При работе с частными производными нужно твёрдо понимать, что в самом их обозначении кроется опасность: частная производная функции

по

зависит не только от того, какая функция в рассматриваемой области принята за координату

, но в ещё большей мере от того, как выбраны прочие координаты. Например, на плоскости с координатами

частная производная
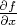
функции

равная нулю, но частная производная
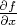
той же функции точки плоскости по той же переменной

в системе координат

, где

, равна

.
Я что-то совсем не понимаю смысла написанного. Как получаются разные значения частной производной по одной и той же первой переменной

? Мы как-то по разному относимся к обозначениям? Сначала как к числам, а в какой-то момент как к функциям? Может кто-нибудь сделать выкладки, из которых получаются два различных числа?
-- 29.09.2018, 19:46 --Имеется ввиду следующее?

в


в

т.к.
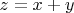
, ну то есть отсюда и выразили, чтобы получить выражение для
