Элемент

принадлежит множеству
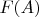
. Если

- это множество, то надо ставить знак "содержится".
Я имел в виду содержательный ответ, а Вы дали тривиальный: просто прочитали формулу. В результате за Вас ответил
Slav-27. Это нехорошо в первую очередь для Вас.
И в рассматриваемой ситуации символ "

" будет независимо от природы

. Тем более, что в теории множеств никаких объектов, кроме множеств, нет вообще. (Бывают теории множеств с атомами, которые не являются множествами, но не заморачивайтесь этим.)
Где можно посмотреть примеры доказательства подобных утверждений?
Каких "подобных"? Если Вы об обсуждаемом утверждении, то оно столь очевидно, что вряд ли Вы его где найдёте в явно написанном виде, кроме контрольных вопросов на понимание определения.
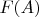
- все значения функции, которое она принимает на множестве

.
Не "все значения", а "множество всех значений", или, короче, образ множества

.