Задача выглядит таким образом: пусть

- векторное поле на сфере

, не имеющее нулей в верхней половине сферы (при

), пусть

- угол, образуемый вектором

и вектором, касательным к экватору

, в точке

;

- единичная окружность с центром в начале координат. Докажите, что кривая
![$\varphi:[0,2\pi]\to\omega\subset\mathbb{R}^2\setminus\{(0,0)\}$ $\varphi:[0,2\pi]\to\omega\subset\mathbb{R}^2\setminus\{(0,0)\}$](https://dxdy-03.korotkov.co.uk/f/e/0/f/e0fb46cba8bfac6787e92b3248f4095882.png)
гомотопна кривой
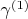
.
(
![$\gamma^{(k)}:[0,2\pi]\to\mathbb{R}^2\setminus\{(0,0)\}$ $\gamma^{(k)}:[0,2\pi]\to\mathbb{R}^2\setminus\{(0,0)\}$](https://dxdy-04.korotkov.co.uk/f/b/c/9/bc9f4a344fb7fc1181bf41e05adae4b982.png)
- замкнутая кривая, заданная формулой

. Считаем известным, что кривые
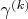
с различным

не гомотопны друг другу)
Вообразим сферу с центром в начале координат, пусть ее северный полюс будет в т.
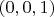
(верхняя половина сферы, нулей нет). Тогда плоскость

проходит через экватор сферы. На этом экваторе в каждой точке

рассмотрим угол между касательной к экватору и вектором

(вектор может быть направлен в любую сторону, в том числе совпадать с касательным к экватору в этой точке, или быть противоположным ему). Через южный полюс сферы спроецируем ее противоположную полусферу на плоскость (параллельную

и касающуюся сферы в т.
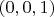
(северный полюс), получим круг на котором имеется векторное поле без нулей. Перенесем этот круг на плоскость

, центром в начало координат и рассмотрим его. На этом круге будет находиться наш касательный к экватору в точке

(теперь находящейся на границе круга, пусть длина вектора этого равна 1) и вектор

, перенесем эти оба вектора началом векторов в начало координат и прокрутим тот, который был касательным к экватору против часовой стрелки. Пока он прокручивается, второй вектор тоже движется, вырисовывая концом некоторую кривую (которая будет непрерывной) (этот момент мне кажется на интуитивном уровне, т.к. векторы близких точек должны менять направление плавно. Ну и т.к. векторное поле без нулей, то и скачков быть не может))(Тут все верно?). Осталось понять почему эта кривая гомотопна именно
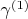
(нужно опираться на то, что

, т.е. кривая замыкается ?).