Задача из Коткина Сербо

[pogulyat_vyshel]

Задача 4.20 из Коткина Сербо по классической механике : требуется найти первые интегралы системы с лагранжианом:

$$L=\frac{m}{2}(\dot r^2+r^2\dot \theta^2+r^2\dot\varphi^2\sin^2\theta)-G\dot\varphi\cos\theta.$$

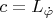
В ответе имеется один очевидный интеграл $c=L_{\dot\varphi}$ а другой какой-то дикий, зависящий от времени.
Я написал гамильтониан и у меня отделилась переменная $\theta$. Т.е. второй первый интеграл это функция $F=F(\theta,p_\theta,c)$ и система интегрируется. Я что-то не так понял?

-- 19.09.2018, 13:24 --

а ,да, там еще векторный интеграл выписан, что-то типа вектора Лапласа. Это значит, что там 4 независимых интеграла в этой задаче?

[amon]

pogulyat_vyshel в сообщении #1340118 писал(а):

Это значит, что там 4 независимых интеграла в этой задаче?

С моей рабоче-крестьянской точки зрения - да, не меньше четырех. Написана функция Лагранжа для магнитного монополя. Поле монополя сферически симметрично, значит как минимум сохраняется энергия и вектор углового момента. Единственная незадача - монополей пока не нашли.

[pogulyat_vyshel]

Понятно. Избыточный набор первых интегралов обычно приводит ко всяким веселым вещам как например в задаче Кеплера: все ограниченные траектории периодичны

[amon]

pogulyat_vyshel в сообщении #1340179 писал(а):

Избыточный набор первых интегралов обычно приводит ко всяким веселым вещам

В задаче (классической) о монополе возникает какое-то забавное движение по поверхности конуса (ось конуса вдоль вектора углового момента). Деталей, увы, не помню.

[Red_Herring]

amon в сообщении #1340169 писал(а):

С моей рабоче-крестьянской точки зрения - да, не меньше четырех. Написана функция Лагранжа для магнитного монополя. Поле монополя сферически симметрично, значит как минимум сохраняется энергия и вектор углового момента.

Вообще-то так сразу здесь сферическая симметрия не видна

pogulyat_vyshel в сообщении #1340179 писал(а):

Избыточный набор первых интегралов обычно приводит ко всяким веселым вещам как например в задаче Кеплера: все ограниченные траектории периодичны

В задаче с любым центрально симметричным потенциалом $V(r)$ те же 4 первых интеграла: угловой момент и энергия, но только для $V(r)=ar^2$ и $V(r)=ar^{-1}$ все ограниченные траектории периодичны.

[amon]

Red_Herring в сообщении #1340213 писал(а):

Вообще-то так сразу здесь сферическая симметрия не видна

Как я понимаю, для этого авторы такую экзотику как монополь Дирака и использовали - что бы студентам механика медом не казалась. А я воспользовался замшелыми остатками сакрального знания о нем.

[pogulyat_vyshel]

Red_Herring в сообщении #1340213 писал(а):

но только для $V(r)=ar^2$ и $V(r)=ar^{-1}$ все ограниченные траектории периодичны.

это потому, что тут первых интегралов 5