То есть получается следующее: физическая интерпретация не соответствует природе математического объекта, но особо ей не противоречит, так что можно использовать и в определённых границах свободно переключаться с одного на другое?
Да, примерно так.
Тут упоминался учебник
Савельева, там в первых параграфах есть отдельный параграф на эту тему. Рекомендую найти и прочесть.
Никакая физическая реальность пока ещё в точности не соответствует никакому математическому объекту. Физики мирятся с этим несоответствием, загоняя его "в пределы погрешности". (В практических задачах погрешность устанавливается такой, какая достаточна для практических нужд. В фундаментальных исследованиях погрешность устанавливается наилучшей, которая достижима экспериментальными приборами и методами на сегодняшний день - эта величина переменная и со временем улучшается, однако улучшения крайне трудны и дорогостоящи.) Различные физические теории:
- могут согласовываться с экспериментом довольно грубо, но лучше теории на замену нет - тогда это полагают погрешностью теории;
- могут согласовываться с экспериментом в рамках или на грани экспериментальной погрешности - тогда это область активных исследований;
- могут согласовываться с экспериментом прекрасно на протяжении десятилетий или столетий, укладываясь в экспериментальную погрешность, как бы она ни уменьшалась (иногда на много порядков!) - тогда это прекрасные теории.
Примеры таких теорий: квантовая физика, ОТО; теория тяготения Ньютона на протяжении с 17 по конец 19 века.
Рассмотрим пару примеров:
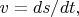

С точки зрения математики, эти соотношения возникают из конечных соотношений типа


Насчёт конечных соотношений физики и математики вполне согласны, но хочется "отбрасывать слагаемые высших порядков малости", упрощая выкладки. С точки зрения математики, это можно сделать, если взять пределы


Но физики знают, что не могут взять таких пределов. При устремлении

наступает момент, когда из-за квантовой неопределённости погрешность

начинает не уменьшаться, а расти. (На самом деле, такой момент часто наступает раньше из-за других причин.) При устремлении

мы рано или поздно натыкаемся на атомарную структуру вещества, и вместо гладкой функции

опять же получается ерунда. Так что физики смотрят на эти формулы как на некоторую идеальную картину, в которую хочется поверить, но до конца не верится. Они применяют формулы
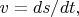

в
их области применимости: при достаточно больших интервалах времени, при достаточно больших элементах объёма. Помнить про область применимости - естественно для физика, но математики привыкли смотреть на любой факт как на верный всегда и везде.
-- 14.09.2018 20:37:53 --То есть, физики работают с

как с математическим объектом, доводят выкладки до точного математического вывода, а потом смотрят: а не вышел ли этот вывод за границы применимости, как их представляют себе физики? Границы применимости удобно представлять себе как интервалы на шкалах физических величин. Например, мы знаем, что межатомные расстояния в твёрдом теле - порядка

Тогда мы можем пользоваться выводами, сделанными из формулы

если эти выводы касаются масштабов в миллиметры, метры, километры.