Содержит подграф, гомеоморфный

или
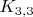
.
Доказательства критерия планарности Понтрягина-Куратовского либо длинны, либо трудны. Существуют другие критерии планарности, но как понимаю с ними тоже не так все просто. И в части алгоритмической (вычислительной) сложности. И это только то, что касается вложимости графа в плосокость. Если мы говорим о каких то других поверхностях, то там, наверное, еще все сложнее и может быть поэтому есть актуальный интерес к вопросу, озвученному в начале темы?
И еще. Сейчас модно начинать курсы алгебраической топологии с идеи вложимости графов в поверхности (например, Элементы комбинаторной и дифференциальной топологии, Прасолов В.В.). Может не просто так, видимо это как то влияет на получение серьезных результатов в алгебраической топологии?



