Последовательность функций

[Charlz_Klug]

Проверьте, пожалуйста, доказательство.

Задача:
Покажите, что последовательность функций $x_n(t) = n^2te^{-nt}$ на отрезке $[0,1]$ сходится к нулевой функции поточечно (т.е. при каждом фиксированном $t \in [0,1]$), но не сходится равномерно на отрезке $[0,1]$.

Доказательство:
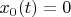
Как я понял, для того чтобы последовательность функций равномерно сходилась к $x_0$ нужно чтобы для всякого $\varepsilon > 0$ нашлось натуральное число $n_0(\varepsilon)$ такое, что $\rho (x_n, x_0) < \varepsilon$ для всех $n \geqslant n_0(\varepsilon)$. В этой задаче $x_0(t) = 0$. Про метрику ничего не сказано, поэтому я возьму метрику такую: $\rho (x(t), y(t)) = \max\limits_{t \in [0,1]} |x(t) - y(t)|$.
Про поточечную сходимость:
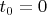
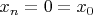
Зафиксирую $t$ взяв некоторое $t_0=0$, тогда $x_n = 0 = x_0$ действительно сходится. Если взять $t_0 \in (0,1]$, то получаем последовательность $x_n = \dfrac {n^2t_0} {e^{nt_0}}$. Устремляю $n \to \infty$ и раскрываю неопределённость методом Лопиталя:

$$\lim\limits_{n \to \infty}\dfrac {n^2t_0} {e^{nt_0}} = \lim\limits_{n \to \infty}\dfrac {2nt_0} {t_0e^{nt_0}} = \lim\limits_{n \to \infty}\dfrac {2n} {e^{nt_0}} = \lim\limits_{n \to \infty}\dfrac {2} {t_0e^{nt_0}} = 0.$$

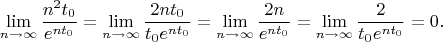
Сходится к $x_0$.
Про равномерную сходимость: опять же воспользуюсь методом Лопиталя:

$$\lim\limits_{n \to \infty}\dfrac {n^2t} {e^{nt}} = \lim\limits_{n \to \infty}\dfrac {2nt} {te^{nt}} = \lim\limits_{n \to \infty}\dfrac {2n} {e^{nt}} = \lim\limits_{n \to \infty}\dfrac {2} {te^{nt}}.$$

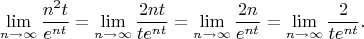
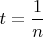
Но в этом случае я могу варьировать $t$. Поэтому я выберу такое $t=\dfrac{1}{n}$, тогда

$$\lim\limits_{n \to \infty}\dfrac {2} {te^{nt}} = \lim\limits_{n \to \infty}\dfrac {2} {\dfrac {1}{n} e^{n \frac {1}{n}}} = \lim\limits_{n \to \infty}\dfrac {2n} {e}.$$

А последнее выражение в этом случае стремится к бесконечности. Отсюда делаю вывод, что равномерной сходимости нет.

[Otta]

Charlz_Klug в сообщении #1331430 писал(а):

Про равномерную сходимость: опять же воспользуюсь методом Лопиталя:

Основания? Есть какие-то признаки равномерной сходимости по Лопиталю?
Пользуйтесь стандартными признаками/критериями/определением.

[thething]

Charlz_Klug в сообщении #1331430 писал(а):

Про метрику ничего не сказано,

И не должно, это просто задача на исследование равномерной сходимости по определению, без отсылки к метрическим пространствам (хотя формально с этой метрикой Вы правы). Так что исследуйте на максимум $\left\lvert x_n(t)-x_0(t)\right\rvert$ на отрезке $[0,1]$.

Ваш способ тоже можно докрутить до противоречия с равномерной сходимостью, если сперва выбрать последовательность $t_n$, а потом, безо всяких Лопиталей заметить, что на ней нужный модуль всяко больше $\frac{1}{e}$.

[Charlz_Klug]

Otta, а для поточечной сходимости метод Лопиталя подойдёт?

-- 09.08.2018, 20:21 --

thething в сообщении #1331437 писал(а):

Так что исследуйте на максимум $\left\lvert x_n(t)-x_0(t)\right\rvert$ на отрезке $[0,1]$.

Я разве по-другому сделал?

-- 09.08.2018, 20:23 --

thething в сообщении #1331437 писал(а):

Ваш способ тоже можно докрутить до противоречия с равномерной сходимостью, если сперва выбрать последовательность $t_n$, а потом, безо всяких Лопиталей заметить, что на ней нужный модуль всяко больше $\frac{1}{e}$.

Действительно, спасибо!

[thething]

Charlz_Klug в сообщении #1331447 писал(а):

Я разве по-другому сделал?

Ну, в точку максимума-то Вы попали чисто случайно, но потом какого-то Лопиталя приплели. А задача-то на тупое исследование функции с помощью производной, либо на получение противоречия с определением на языке $\varepsilon-N$

[Charlz_Klug]

thething в сообщении #1331449 писал(а):

А задача-то на тупое исследование функции с помощью производной, либо на получение противоречия с определением на языке $\varepsilon-N$

Не увидел, да. Спасибо! Тогда беру производную от $x_{n}$ по $t$: $x_{n}'(t) = \dfrac{n^2 e^{nt}-n^3 t e^{nt}}{e^{2nt}}$. Приравниваем $x_{n}'(t) = 0$ и получаем $t = \dfrac{1}{n}$. Подставим теперь $t = \dfrac{1}{n}$ в $x_n(t)$, получаем $x_n(t) = \dfrac{n^2 \dfrac{1}{n}}{e^{n \dfrac{1}{n}}} = \dfrac{n}{e}$. То есть, с ростом $n$ максимум $x_n$ тоже будет лишь возрастать и равномерной сходимости не будет.

[DeBill]

Charlz_Klug
Обратите внимание: максимум оказался равным $\frac{n}{e}$. Как это согласуется с Вашим "Лопиталем" (у Вас там - в 2 раза больше)?

[Charlz_Klug]

DeBill, не могу знать. В принципе мой "Лопитальный" максимум может быть гораздо больше чем просто $\frac{n}{e}$. У меня же получилось $\lim\limits_{n \to \infty}\dfrac {2} {te^{nt}}$, ничто не мешает взять, например $t=\dfrac{1}{n^3}$. Тогда будет стремление к $2n^3$. Наверно, то, что я принимал $t$ за константу и привело к такому результату.

[DeBill]

Charlz_Klug
Именно так .

[Charlz_Klug]

DeBill, большое спасибо!