Для положительных рациональных

и

,

,

найдите без калькулятора

такое, что при

верно неравенство:

Перепишем неравенство в виде

Сделаем замену переменных

,

. Получим

.
Здесь имеется только два (?) положительных корня.

. Тогда подходит
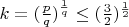
, т.к.

,

.
Если идея верна (?), то дальше возможна арифметика без калькулятора.
Вопрос: верны ли такие рассуждения?
(Надо перепроверить знак на бесконечности; возможно там знак другой.)