Обычно, формулу Эйлера применяют для доказательства отсутствия планарности графа, используя рассуждение от противного.
Классический пример - доказательство того, что

(один из двух графов, фигурирующих в теореме Понтрягина-Куратовского) не планарен.
Пусть

планарен. Тогда
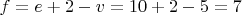
. Но каждая грань окружена не менее чем тремя ребрами, а каждое ребро разделяет две грани.
Поэтому

, т.е.
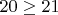
- противоречие.
-- 19 июл 2018, 07:54 --gogoshik
Вы про теорему Куратовского слышали?
Разумеется, имеет смысл начинать с этого критерия.
Однако, проверка наличия/отсутствия подграфов, стягиваемых к

либо
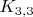
не всегда простая задача. В отличие, например, от критерия эйлеровости.
Поэтому иногда проще воспользоваться оценкой с помощью формулы Эйлера.



