Тут ясно, что поскольку q по меньшей мере равно двум, то
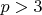
, чтобы выполнялось

- но тогда первое слагаемое нечетно, то есть должно быть

.
Просто проверим явно, что

не подходит:

. Можно перебором, а можно заметить, что у функции в левой части этого уравнения при
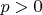
один минимум (нуль производной определяется точкой пересечения экспоненты и правой ветви параболы), при этом при

она равна 24, а при

- отрицательна. Так что минимум лежит где-то между 2 и 9, а при больших значениях функция монотонно возрастает, следовательно, при целых аргументах она не принимает значения 9.
Таким образом,

. То есть решения (если таковые имеются) записываются в виде

.
Так как

- нечетно, то

, где

- некоторое натуральное число. Но

(для любого

!). Следовательно,

.
С другой стороны,

, а

.
Отсюда мы заключаем, что

, т.е. возможное решение может иметь вид

.
В явном виде:

.
Итак, теперь равенство по модулю 6 (а, следовательно, 2 и 3) соблюдается автоматически, и надо только найти подходящую пару

. Но тут строгая математика пасует - или это я еще не набрел на нужное решение (основание модуля?).
_________________________________________________________
Уходя от целочисленной математики, можно заметить, что

, причем разность равна строго

, которая при росте аргументов много меньше других слагаемых, т.е. легко установить (анализируя аналогично второму абзацу этого сообщения), что область значений

лежит рядом (с большей стороны) с решением уравнения

, что эквивалентно

.
Это уравнение трансцендентно, так что все это разве что облегчает поиск решений перебором: при выбранном

есть смысл рассматривать очень ограниченный набор

: простые числа вида

, б
ольшие решения указанного уравнения, причем только ближайшие.
Но насколько ближайшие? В первую очередь, обратим внимание, что мы используем здесь решение этого уравнения

. Но тогда

, а значит,

Если

, то чему равно

? Функция эта, очевидно, монотонно возрастает, поэтому как только мы превысим

, это будет означать, что дальше дальше решений уравнения не будет.

Так как мы установили, что

, а

, то

. Таким образом, подходящее значение

не может превышать

(!). Иными словами - если при данном

есть подходящее значение

, то оно равно округлению вверх решения уравнения

.
Например, для

получаем

, то есть может подойти только

, но оно равно 5 по модулю 6, так что отпадает.
На самом деле решение уравнения

отличается от решения

на одну стотысячную, поэтому мои рассуждения совсем нестрогие, даже чересчур щедрые и относятся уже не к математике, а оптимизации программы-перебора.
Но можно сделать следующий вывод: если существует решение исходного уравнения, то решение уравнения

должно быть "почти целым", причем обязательно округляться в большую сторону:

- это еще одна оптимизация перебора: достаточно довести дихотомию до момента, когда интервал поиска меньше единичного, а целое значение либо внутри него, либо вблизи правой границы. Это целое значение и есть кандидат на

при данном

, его (и только его) надо подставлять для проверки.
_________________________________________________________
Проверка проверкой, но как доказать строго, пока не ясно.



