Бескоорд. выражение для дифференциала векторного отображ-ия

[Geen]

_hum_ в сообщении #1322046 писал(а):

правда, при условии ее дифференцируемости

Этого недостаточно (каустики, линзы). А по Вашему описанию даже этого нет.

_hum_ в сообщении #1322046 писал(а):

принципиальная? Если да, то подскажите, пожалуйста, в чем.

Один множитель потерян в одном слагаемом.

[arseniiv]

Так, мне смутно кажется, что я где-то сделал гигантскую ошибку и насоветовал в итоге бред, но пока не пойму где. Сильно не радуйтесь.

[_hum_]

Насчет поиска градиента функции, наподобие $F = F(\mathbf{s}) = \Big(\pi_\mathbf{r}\big(\mathbf{u}(\mathbf{r}_O, \mathbf{s} )\big)\Big)^2$. Правильно ли я мыслю, и можно ли так делать:
представим приращение направляющего вектора луча $\delta \mathbf{s}$ как $d \mathbf{s} = \mathbf{S}_1d\varphi + \mathbf{S}_2d\theta$, где $\varphi, \theta $ - направляющие углы вектора луча. Тогда, пользуясь линейностью оператора производной отображения, подставим:

$[DF]\delta\mathbf{s} = \nabla F \cdot \begin{bmatrix} \hat{A}_{11} & \hat{A}_{12} \\ \hat{A}_{21} & \hat{A}_{22} \end{bmatrix} \begin{bmatrix} \mathbf{0} \\ \mathbf{S}_1 \end{bmatrix}d\varphi + \nabla F \cdot \begin{bmatrix} \hat{A}_{11} & \hat{A}_{12} \\ \hat{A}_{21} & \hat{A}_{22} \end{bmatrix} \begin{bmatrix} \mathbf{0} \\ \mathbf{S}_2 \end{bmatrix}d\theta$

Выражения при $d\varphi$ и $d\theta$ и будут искомые выражения для компонент градиента функции $F = F(\mathbf{s}(\varphi, \theta))$. Так?

Geen в сообщении #1322059 писал(а):

Этого недостаточно (каустики, линзы). А по Вашему описанию даже этого нет.

ммм... по каустикам в wiki ничего не сказано, насчет того, что это пересечение лучей от одного источника. Вот линза - да. Но наверное такие условия крайне маловероятны.
И я говорил, что условий дифференцируемости достаточно, чтобы найти хотя бы один локальный минимум целевой функции.

Geen в сообщении #1322059 писал(а):

Один множитель потерян в одном слагаемом.

по-вашему, случайно или по непониманию дифференцируемости таких выражений?:)

arseniiv в сообщении #1322067 писал(а):

Так, мне смутно кажется, что я где-то сделал гигантскую ошибку и насоветовал в итоге бред, но пока не пойму где. Сильно не радуйтесь.

хорошо :)

[arseniiv]

Я зря перепугался, см. в конце отчего.

_hum_ в сообщении #1322046 писал(а):

Это как-то связано с диадиками?

Не-не, это просто пары из векторов, но так как они сами векторы, можно забыть про то, что они пары, хотя при вычислениях наверняка будет их координатами брать координаты каждого из элементов пары в удобных для них базисах. А тензорное произведение гораздо больше, чем здесь нужно.

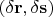
На самом деле я не до конца проверил выражения, но они выглядели линейно по $(\delta\mathbf r,\delta\mathbf s)$, так что всё в порядке и оператор $D\mathbf u$ линейный.

_hum_ в сообщении #1322046 писал(а):

ммм... Матрица оператора, насколько мне известно, сводит его действие к простому умножению, а в моем случае некая смесь "умножений" и применений операторов. Или Вы имеете в виду, что я не до конца их разложил, и потому получились "блочные формы"?

Да, в некотором смысле не до конца — $с\mathbf x$, $(\mathbf x\cdot\mathbf u)\mathbf v$ — линейные операторы от $\mathbf x$, но представлять их как-то иначе в терминах $\mathbf x$, а не его координат, более коротко не выйдет.

_hum_ в сообщении #1322046 писал(а):

Если так, то какой раздел математики такими штуками занимается?

С моей низенькой колокольни это выглядит в основном практическим занятием «представить одно в другом виде». Ну, кроме работы с матрицами, состоящими из операторов, векторов и прочего. Будь объекты все одного сорта (только операторы), и матрицы одного размера, это оказался бы просто модуль (как векторное пространство, но не над полем, а лишь кольцом), но вряд ли вам из их линейной алгебры понадобится что-то особое кроме слова «да, так можно (если не забывать о некоммутативности умножения)». Хотя если обобщать, это получается интересная структура (которую образуют и всевозможные матрицы над некоторым полем, но тут опять будет не поле) типа категории, но с множеством дополнительных свойств. Но для практики-то логично вообще всё разложить до конца, а это промежуточное представление особо не трогать.

Если всё же захочется в выкладках всё-таки использовать,

_hum_ в сообщении #1322046 писал(а):

Меня больше другое волновало - как реально с такими конструкциями работать можно с целью получить простое компактное легко вычислимое выражение (ведь мне нужно будет его использовать в численных методах) - например, насколько для таких "матриц" справедливы свойства, что и для обычных (формулы перемножения, например), можно ли выносить "за скобки" и т.п.

то складывать и умножать на скаляр всё это можно как обычно, а умножать только с учётом некоммутативности — чтобы в произведениях элементы левой матрицы стояли левее элементов правой; очевидные ограничения на размеры сомножителей в этом помогут. Ассоциативность умножения таких матриц останется (раз умножение их элементов, когда оно определено, ассоциативно).

Единственное, что портится, и от чего я поднял панику — это то, что квадратные матрицы над некоммутативным кольцом не образуют алгебру над ним же. Ну а нам этого и не нужно; нам достаточно того, что они образуют алгебру над тем кольцом, над которым алгебру образуют элементы. В данном случае это означает, что матрицы над линейными операторами не образуют над ними алгебру (и не надо, действительно), но образуют над вещественными числами (над которыми линейные операторы сами алгебра). Как я понимаю, вы и не собирались ничего хорошего ждать от умножения таких матриц на «скаляр», где «скаляр» — оператор, и вообще не собирались такое умножение нигде проводить, и я даже не вижу, как бы оно могло возникнуть в подобной вашей задаче. Так что всё ок.