Задача из I тома мат. анализа Зорича

[Paul Ivanov]

Задача звучит так:
имеется непрерывное отображение $f : [0,1] \to [0,1]$ такое, что $f(0) = 0, f(1) = 1$.
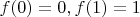
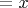
Нужно доказать, что если $\underbrace{f\circ\dots\circ f}_{n}(x)$ $=x$ для некоторого $n\in\mathbb{N}$, то $f(x)\equiv x$.
1. Я уже доказал это утверждение для $n = 2$.
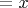
2. Также несложно показать, что если $\underbrace{f\circ\dots\circ f}_{n}(x)$ $=x$, то $\forall\, k\,(k \in \left\lbrace1,2,...,n\right\rbrace \Rightarrow$ $\underbrace{f\circ\dots\circ f}_{k}$ - строго монотонная функция на $[0,1]$$)$.
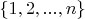
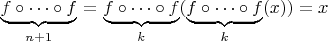
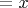
3. По индукции, предполагая, что утверждение верно для $\left\lbrace1,2,...,n\right\rbrace$ несложно показать, что оно также верно для $n+1$, если $n+1$ - чётное число. Ведь тогда $\underbrace{f\circ\dots\circ f}_{n+1}$ $=$ $\underbrace{f\circ\dots\circ f}_{k}(\underbrace{f\circ\dots\circ f}_{k}(x))=x$ а отсюда из 1. следует, что $\underbrace{f\circ\dots\circ f}_{k}(x)$ $=x$ для некоторого $k \in \mathbb{N}$, из чего согласно индукционному предположению следует основное утверждение.
Непонятно, как с помощью всего этого доказать необходимое для нечётного n. Больше никаких идей кроме использования 1. 2. и 3. нет...

[iifat]

Собственно, аналогичный шаг индукции работает для любого составного $n+1$. Хотя да, этого тоже мало.

[ewert]

Индукция тут ни к чему и не при чём, всё гораздо прямолинейнее. Множество точек, в которых $f(x)=x$, замкнуто. Соответственно, дополнение к нему -- открыто. Берём любой интервал из совокупности, образующей это дополнение. Что можно сказать про результат любого количества итерирований на этом интервале? (учитывая уже известную монотонность функции)

[Paul Ivanov]

ewert в сообщении #1320397 писал(а):

Индукция тут ни к чему и не при чём, всё гораздо прямолинейнее. Множество точек, в которых $f(x)=x$, замкнуто. Соответственно, дополнение к нему -- открыто. Берём любой интервал из совокупности, образующей это дополнение. Что можно сказать про результат любого количества итерирований на этом интервале? (учитывая уже известную монотонность функции)

Да, вы правы. Всё замечательно получается. Если довести вашу идею до конца, то нужно просто показать, что найдётся подобный интервал, у которого концы принадлежат замкнутому множеству и тогда любая итерация будет либо последовательно уменьшать, либо последовательно увеличивать значение по сравнению с предыдущей итерацией и при этом не будет выводить взятую точку за границы данного интервала.
Спасибо!

[ewert]

Я бы только один момент подправил.

Paul Ivanov в сообщении #1320380 писал(а):

2. Также несложно показать, что если $\underbrace{f\circ\dots\circ f}_{n}(x)$ $=x$, то $\forall\, k\,(k \in \left\lbrace1,2,...,n\right\rbrace \Rightarrow$ $\underbrace{f\circ\dots\circ f}_{k}$ - строго монотонная функция на $[0,1]$$)$.

Это избыточно и сбивает с толку. Не очень понятно, как это доказывать. Между тем вполне очевидно, что из исходного тождества (с учётом непрерывности) следует строгая монотонность самой функции. Из чего, естественно, следует и Ваше утверждение, но оно попросту ненужно.