что вам мешает наставить штопоры где надо?
А где надо? По-моему, больше нигде не надо.
Ничего они не смешиваются. ... Формулы теории являются как раз значениями одного из видов термов метатеории (если мы выбрали её теорией первого порядка).
Ну да, в этом смысле и смешиваются: Формулы предметной теории являются частью формул мета-теории.
А потом вы зачем-то используете эти термы как формулы самой метатеории.
Не "я использую эти термы как ...", а они посимвольно совпадают с формулами самой мета-теории. Какой в этом криминал?
На деле это будут просто одинаковые имена для разносортных выражений, не более. Вы не можете их отождествлять, а одинаковость имён только путает.
Теории вообще "только именами" и манипулируют. "Самими объектами" могут манипулировать только те, кто работают руками, а не головой. И почему это должно "путать"? Вот формула языка арифметики
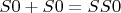
выводима из аксиом арифметики. Мета-теория об этом может сказать так:

. В силу теоремы дедукции отсюда следует

(где

- объединенные по конъюнкции все те аксиомы арифметики, из которых сделан этот вывод). Если мета-теория имеет все те же символы в своей сигнатуре, т.е. способна записывать формулы арифметики как свои, то что ей мешает записать этот же вывод от своего имени, т.е. без штопора вначале строки?
чтобы определить формальную теорию (назовём её предметной теорией), мы должны определить её алфавит, термы, формулы и т.д.
Можно считать, что бОльшая часть этой работы уже проделана при формализации самого исчисления предикатов. Поэтому нормальной мета-теории достаточно доопределить сигнатуру предметной теории и далее можно строить утверждения типа: "если аксиомы будут такими-то, то выводимо будет то-то".
В частности, формулы предметной теории являются объектами, но не формулами метатеории.
Так я ж сам об этом говорил.
Эти самые

и

— это объекты метатеории, которые мы интерпретируем как формулы предметной теории.
Хм. Объекты метатеории нет смысла интерпретировать как формулы предметной теории. Это термы мета-теории интепретируются как её объекты, каковые
и есть формулы предметной теории. Точно так же, как термы арифметики интерпретируются как её объекты - натуральные числа. Нет смысла "интерпретировать" объекты арифметики как натуральные числа, ибо они
и есть натуральные числа.
На этот вопрос можно будет ответить после того, как Вы формально определите метатеорию, в которой определите предметную теорию.
Не вижу в этом такой уж проблемы. Нужно включить в сигнатуру штопор - как символ выводимости, а в аксиоматику - записанные через него теорему дедукции и правило модус поненс. Плюс - всё то, что есть в сигнатуре рассматриваемых предметных теорий (возьмём для примера арифметику), чтобы иметь возможность от имени самой мета-теории говорить о том же, о чём говорят предметные теории. Ну, средства для синтаксического разбора формул предметных теорий тоже конечно потребуются (и непростые), но думаю, что суть не в них.



