Имеем отрезок числовой прямой [0, 1] длины 1. Из этого отрезка мы выбрасываем некое счётное множество точек. Какая будет длина оставшегося кусочного отрезка?
Для подобных "сложных" множеств ввести понятие длины возможно, оно называется - мера Лебега. О ней можно подробно прочитать в учебниках действительного и функционального анализа (но обычно это довольно сложные учебники), но можно также заглянуть в Википедию.
Мера Лебега обладает сигма-аддитивностью (счётной аддитивностью). Это значит, что мера объединения счётного количества непересекающихся множеств равна (бесконечной) сумме мер этих множеств. Каждая точка (а точнее, одноточечное множество) имеет меру (т.е. длину), равную нулю. Поэтому счётное множество точек будет иметь меру
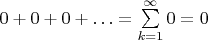
. Да, "сумма счётного количества нулей" обязательно равна нулю, как можно легко понять из определения бесконечного ряда (кстати, найдите это определение и разберитесь, почему так). Поэтому, если мы выбросим из отрезка длиной

счётное множество (например множество точек с рациональными координатами), то оставшееся множество будет иметь меру

.
Ну и вопрос со звёздочкой. Можно ли составить такое не счётное и не конечное множество, после выбрасывания которого из отрезка, длина оставшегося кусочного отрезка (опять же, что такое длина в данном случае) останется равна 1?
Погуглите про канторово множество.



