Разумеется, неправильно.
Вначале обращу внимание, что индекс

у Вас в условии задания пишется сверху. Почему Вы его спускаете вниз, что создаёт путаницу с индексом

?
Вот у Вас есть формула для нормы:

.
Подставьте теперь

вместо

в эту формулу, чтобы найти

. А там потом и до
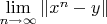
доберёмся.
И ещё вопрос: как Вы поточечный (скорее, лучше говорить "покоординатный") предел находили? Напишите подробно.
Посмотрите ещё вот это
моё объяснение. Оно совсем по другому поводу, но может поможет что-то прояснить, если что-то не понимаете в происходящем.
-- 02.06.2018, 18:03 --Совет из этого объяснения - обращать внимание на
осмысленность записываемых формул - к Вам также относится.
Вот, например, Вы в одном месте написали

. Судя по этой записи,

- это числа (от которых можно взять модуль, а затем супремум). Но в другом месте Вы пишете

, а это намекает, что

- элементы того же метрического пространства, что и

, а именно пространства

, то есть вовсе никакие не числа, а числовые последовательности. То есть или с одной из этих записей, или с другой, или с обоими что-то не то.
Не разобравшись хорошо в смысле всех этих

,

,

,

- какие именно объекты обозначены этими буковками - к решению задачи приступать нельзя. Даже если как-то получится правильный ответ, и даже если правильное решение - решённой такую задачу нельзя будет назвать.