Найти верхний и нижний пределы

[Ivan_B]

Как должно выглядеть решение упражнения вида:
$\varliminf\limits_{n\to\infty}\left(1+\frac{1}{n}\right)^n(-1)^n+\sin\frac{n\pi}{4}$

Из последовательности $\left(1+\frac{1}{n}\right)^n$ множитель $(-1)^n$ выделяет две сходящиеся подпоследовательности с пределами $e, -e$, которые затем смещаются $\sin\frac{n\pi}{4}$ на $-1, 0, 1$ и $-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$. Пределами будут $e-1, e, e+1, -e-\frac{\sqrt{2}}{2}, -e+\frac{\sqrt{2}}{2}$ Минимальный из них $-e-\frac{\sqrt{2}}{2}$
Изначально я такие упражнения решал устно, но сейчас понял, что если бы мне такое упражнения попалось на экзамене, я бы не знал что писать.
Или такого словесного описания должно быть достаточно?

[Xaositect]

Вряд ли. Надо использовать определение нижнего предела. Нижний предел - это инфимум множества частичных пределов. То есть надо доказать, что $-e-\frac{\sqrt 2}{2}$ является частичным пределом, а никакая точка меньше $-e-\frac{\sqrt 2}{2}$ частичным пределом не является.

[slavav]

Ivan_B, вы не нашли верхний предел.
Надо действовать более формально. Например вы ищете все возможные суммы элементов множеств $\{-e, e\}$ и $\{0, \frac{\sqrt 2}{2}, 1, -\frac{\sqrt 2}{2}, -1\}$. Всех возможных таких сумм - десять штук. Вы отбрасываете четыре. Почему?

[ewert]

Xaositect в сообщении #1316435 писал(а):

Надо использовать определение нижнего предела. Нижний предел - это инфимум множества частичных пределов.

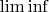
Это как сказать. Вообще-то нижний предел по определению -- это предел инфимумов (откуда и столь любимое за бугром обозначение $\liminf$ вместо нормального, человеческого $\varliminf$). То, что это одно и то же -- есть некоторая стандартная теорема. И такое определение выгоднее потому, что инфимумы, в отличие от частичных пределов вообще, гораздо обозримее.

Конкретно здесь. Если временно отбросить первый "экспонентный" множитель, то очевидно, что последовательность распадётся на не более чем восемь (не важно, на сколько именно) чередующихся стационарных подпоследовательностей. Инфимумы для такой упрощённой последовательности определяются по той подпоследовательности (не важно какой из них), для которой значение минимально, т.е. равно $-1-\frac{\sqrt2}2$. После возврата множителя $(1+\frac1n)^n$ для любой подпоследовательности с таким стационарным значением инфимумы будут стремиться к $-e-\frac{\sqrt2}2$, а для подпоследовательностей с другими стационарными значениями будут заведомо выше. Следовательно, и общий инфимум будет стремиться к тому же.

Добивка. Есть соблазн воспользоваться возрастанием последовательности $(1+\frac1n)^n$ (из чего следует, что инфимумы вообще постоянны). Это -- вредный соблазн: факт и случаен, и нетривиален, и почти не помогает. Важна лишь сходимость этой последовательности.

[thething]

Ivan_B в сообщении #1316424 писал(а):

Или такого словесного описания должно быть достаточно?

Достаточно, если укажете, что выписали все частичные пределы (и других быть не может) и сошлётесь на теорему о том, что нижний предел -- есть наименьший среди всех частичных пределов.

[Ivan_B]

Столько ответов! Огромное Вам всем спасибо!

Xaositect в сообщении #1316435 писал(а):

надо доказать, что $-e-\frac{\sqrt 2}{2}$ является частичным пределом, а никакая точка меньше $-e-\frac{\sqrt 2}{2}$ частичным пределом не является.

thething в сообщении #1316461 писал(а):

Достаточно, если укажете, что выписали все частичные пределы

Ничего проще придумать не удалось.
Разделить исходную последовательность на $8$ подпоследовательностей:
$n_k=8k, n_k=8k+1,$ $n_k=8k+2, n_k=8k+3,$ $n_k=8k+4, n_k=8k+5,$ $n_k=8k+6, n_k=8k+7,$
Вычислить предел каждой из них:
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k}\right)^{8k}(-1)^{8k}+\sin\frac{(8k)\pi}{4}=e$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+1}\right)^{8k+1}(-1)^{8k+1}+\sin\frac{(8k+1)\pi}{4}=-e+\frac{\sqrt{2}}{2}$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+2}\right)^{8k+2}(-1)^{8k+2}+\sin\frac{(8k+2)\pi}{4}=e+1$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+3}\right)^{8k+3}(-1)^{8k+3}+\sin\frac{(8k+3)\pi}{4}=-e+\frac{\sqrt{2}}{2}$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+4}\right)^{8k+4}(-1)^{8k+4}+\sin\frac{(8k+4)\pi}{4}=e$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+5}\right)^{8k+5}(-1)^{8k+5}+\sin\frac{(8k+5)\pi}{4}=-e-\frac{\sqrt{2}}{2}$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+6}\right)^{8k+6}(-1)^{8k+6}+\sin\frac{(8k+6)\pi}{4}=e-1$
$\lim\limits_{k\to\infty}\left(1+\frac{1}{8k+7}\right)^{8k+7}(-1)^{8k+7}+\sin\frac{(8k+7)\pi}{4}=e-\frac{\sqrt{2}}{2}$
Для любой точки $a$, отличной от полученных предельных точек можно выбрать окрестности этих предельных точек, которые не будут содержать точку $a$. Эти окрестности будут содержать все элементы исходной последовательности за исключением первых $N$. Поэтому точка $a$ не может быть частичным пределом исходной последовательности.

ewert в сообщении #1316452 писал(а):

Если временно отбросить первый "экспонентный" множитель

Не могу придумать как можно это обосновать.

slavav в сообщении #1316437 писал(а):

Вы отбрасываете четыре. Почему?

Я разбиваю последовательность на две подпоследовательности. Затем полученные подпоследовательности разбиваю дальше. Первое разбиение накладывает ограничение на $n$(его четность) которое накладывает ограничение на значение $\sin\frac{n\pi}{4}$