Уважаемые коллеги, очень прошу Вас помочь мне ещё с одним ребусом, который представляю Вашему вниманию. Пусть

и

-- две различные точки области

риманового многообразия


где

и

Будем предполагать, что

компакт. Обозначим через

-- геодезическое расстояние между точками

и

на
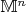
(= инфинум длин всех кусочно-гладких кривых, соединяющих точки

и

на
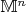
). ВОПРОС. Можно ли построить две такие кусочно-гладкие кривые
![$\alpha:[0, 1]\rightarrow {\Bbb M}^n$ $\alpha:[0, 1]\rightarrow {\Bbb M}^n$](https://dxdy-04.korotkov.co.uk/f/7/2/d/72d347cb246dfaf0cec6e13cae33317982.png)
и
![$\beta:[0, 1]\rightarrow {\Bbb M}^n,$ $\beta:[0, 1]\rightarrow {\Bbb M}^n,$](https://dxdy-02.korotkov.co.uk/f/5/c/3/5c3592be63e54a88abbeb845cac5d05a82.png)
что: 1)


при
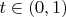
и



при
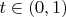
и

2) геодезическое расстояние

между образами (носителями) кривых
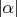
и

не меньше

?
На плоскости
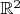
и даже пространстве


такой результат верен. Если мы рассмотрим произвольную ограниченную область

и соединим заданные точки

и

обычной прямой, то несложно выделить отрезки, лежащие на этой прямой, с указанным свойством. В частности, поскольку область

ограничена, в силу общих теорем о связности множеств (см., напр., теорема 1, пункт I,

гл. 5, Куратовский, Топология, т. 2) такая прямая пересекает границу области. Что будет происходить на многообразии - непонятно. Буду рад любым комментариям и советам !



