wooddii писал(а):
Поле ведь изоморфно

Оно изоморфно только при простых

. Но 4 - не простое число, поле из 4 элементов - это не класс вычетов по модулю 4, иначе элемент 2 в нем был бы необратим. Не поленитесь, откройте учебник, почитайте как строятся конечные поля. И найдите как строится поле из 4 элементов, или постройте его сами. Без знания основ вы не сможете решать такие задачи и будете все время делать в них глупые ошибки
Да, только тогда, когда

простое,
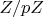
будет полем, поэтому и написал собственно

.
Поле строится присоединением корня неприводимого многочлена, это мне известно.
Из четырех элементов, например, присоединением корня неприводимого полинома степени 2.
Я в условии указал, как оно строится в общем виде.
А откуда взялось 4 собственно?
В качестве контр-примера?
-- 27.05.2018, 01:59 --Еще путаюсь, думаю одно, пишу другое иногда)
-- 27.05.2018, 02:01 --Однако ведь, если

такое, что

не делится на 3, то утверждение верно и доказательство более-менее сносное?
-- 27.05.2018, 02:18 --Ну да, так получается.
То что выше писал, да, ересь, прошу прощения.
На ночь глядя не пойми что несу.
Поле из 4-х элементов,

,

- в точности корень неприводимого полинома, на основе которого построили расширение.
Никаких двоек и троек там нет, там есть только 0, 1,

(корень многочлена

) и

.
Вроде бы все до конца осознал теперь.
Спасибо!



