
?
Отнюдь. А если бы и так было, Вы, очевидно, все равно не понимаете почему.
Так как многочлен

неприводим в
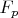
.
Ох, тяжко отвечать, коль не проходили мы этого всего)
А почему он неприводим ? Это же и значит, собственно, что корня из

нет.
И вообще... как же я буду Вам помогать, если, как выясняется, вы базового материала не проходили, и того, и этого, и третьего ?
Несколько дней назад я отвечал тоже на вопрос по конечным полям, там есть список литературы. Поищите. Почитайте. А то, я вижу, у Вас в голове какие-то обрывочные сведения.
Ну, допустим, данную задачу я Вам могу объяснить, кое-как. Но вообще необходимость улучшения знаний имейте в виду.
(Знаю я, что есть заведения, и не одно, где людей учат то ли алгебре с уклоном в криптографию, то ли криптографии с элементами алгебры, но, в общем, с пятого на десятое.)
Знаете ли Вы, как устроена мультипликативная группа

?



