RIP писал(а):
Ваши условия эквивалентны тому, что

сохраняет скалярные произведения.
Поясните, пожалуйста, этот момент подробнее.
Мне вот что непонятно. Надо доказать, что

. Имеем


можно заменить на

по условию. Но почему

можно заменить на

?
Добавлено спустя 18 минут 59 секунд:
AGu, спасибо за
ссылку. Благодаря ей, кстати, выяснилось, что я упустил важное условие на

--- сюрьективность (либо строгую выпуклость). Как показывает пример в тексте по этой ссылке, условие на сюрьективность (строгую выпуклость) существенно: без него линейности может не быть даже в случае
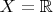
и

.
Хотя в случае предгильбертовости пространств

и

строгая выпуклость выполняется автоматически




