Исследование аналитической функции

[MChagall]

Исследовать полную аналитическую функцию (выбрать начальный элемент; определить, по каким кривым продолжается; сколько элементов с центром в данной точке и как они отличаются, описать изолированные особые точки) $(1-z^2)^{\frac{1}{3}}$ (не нашёл значка кубического корня).

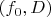
В качестве начального элемента предлагаю взять $(f_0, D)$, где $D$ единичный круг, $f_0(z)=1+\sum\limits_{n=0}^{\infty}C_{\frac{1}{3}}^n(-1)^nz^{2n}$. Продолжается вдоль путей, не проходящих через точки $z=\pm 1$, но как это показать? Представить функцию в виде интеграла $\int\limits_{0}^{z}\frac{-2zdz}{3(1-z^2)^{\frac{2}{3}}}$ и сказать про его существование на указанных непрерывных кривых?
Далее как в предыдущей задаче https://dxdy.ru/post1306785.html#p1306785 рассмотреть что происходит при обходе через точки $z=\pm 1$. Отсюда сделать вывод про количество элементов. Ну и про особые точки здесь же выйдет.
Верный путь или где-то не то?

[Aritaborian]

(Кубический (и не только кубический) корень в ТеХе)

\sqrt[b]{a} даст вам искомое: $\sqrt[b]{a}$.