Докажите, что не существует конечной группы

такой, что

- некоторые её подгруппы со свойствами:

,

.

, при
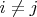

Понятно, что

сопряжениями, при этом элемент из

оставляет саму

месте и меняет все остальные

на другие сопряжённые им подгруппы, возможно есть шанс доказать, что при этом они должны именно переставляться, а не просто переходить в другие подгруппы. Можно записать какие-то равенства: размер орбиты:

, ещё
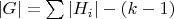
. Но они ничему не противоречат и вряд ли будут.
Сложно понять в каком направлении "лежит" противоречие.