Согласно
интерпретации Брауэра-Гейтинга-Колмогорова (сокращённо - BHK) существование объекта

со свойством

может быть доказано только предъявлением такового объекта. Вопрос заключается в том, что формально означает "предъявление" объекта, для которого мы потом доказываем, что он обладает указанным свойством?
Я рассмотрел такие варианты:
1. Буквальное предъявление
для наблюдения. Сей вариант был признан неприемлемым, ибо теории могут говорить только о теоретических объектах, предъявить которые читателю непосредственно в момент прочтения им учебника никак невозможно. Например, если теория утверждает существование какого-нибудь "нейтрино", то предъявить его для наблюдения хотя и возможно в принципе, но для этого потребуется лаборатория, т.е. сделать это чисто теоретическими средствами (с помощью текста в учебнике) никак не получится. Не говоря уж о предъявлении сугубо абстрактных объектов типа "натуральное число", которые вообще непонятно как можно предъявить для наблюдения.
2. Определение константы в языке теории. Например, можно считать, что существование числа "нуль" доказано уже в силу того, что в языке арифметики Пеано определена константа

. Этот вариант я полагаю приемлемым, но недостаточно общим, ибо есть множество теоретических объектов, для обозначения которых никогда не вводились и скорее всего никогда не будут вводиться константы.
3. Предъявление формулы теории, для которой доказана единственность соответствующего объекта. Т.е. мы должны записать формулу

и доказательства
![$\exists x \forall y~\psi[y|x] \leftrightarrow x=y$ $\exists x \forall y~\psi[y|x] \leftrightarrow x=y$](https://dxdy-01.korotkov.co.uk/f/c/8/7/c871d1d0bfc8f5a657ca47a4dc54ded182.png)
(где
![$\psi[y|x]$ $\psi[y|x]$](https://dxdy-01.korotkov.co.uk/f/4/4/3/443aad94a9476376365dd9da8832e80882.png)
- результат подстановки

вместо всех свободных вхождений

в формулу

, причём если имелись связанные вхождения

в формулу

, во избежание конфликтов они должны быть заменены на какую-нибудь новую переменную) - единственности объекта со свойством

, и
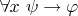
- наличия у этого объекта свойства

.
Этот вариант представляется мне наиболее подходящим, хотя:
а) Он требует, чтобы в теории было определено отношение равенства, удовлетворяющее соответствующим аксиомам.
б) Доказательство единственности предполагает доказательство существования объекта

со свойством
![$\forall y~\psi[y|x] \leftrightarrow x=y$ $\forall y~\psi[y|x] \leftrightarrow x=y$](https://dxdy-02.korotkov.co.uk/f/1/d/5/1d5fcbeecbc49bbcadd33ec52b0bcc1082.png)
, которое, в свою очередь, должно соответствовать BHK. В принципе, это может породить рекурсию доказательств, которая не будет иметь конца. Но я полагаю, что в некоторых случаях эту рекурсию можно будет закончить сведением к пункту 2 - когда доказательство единственности сведётся к доказательству равенства константе: Например, единственность

со свойством

очевидна в силу того, что при подстановке в указанную выше формулу единственности мы получим тавтологию

.
4. Предъявление
класса эквивалентности объектов

, обладающих свойством

. Например, объект арифметики "число два" можно трактовать как множество

(здесь в качестве отношения эквивалентности выступает арифметически доказанное равенство числу, обозначенному замкнутым термом
).
Этот вариант представляется мне несоответствующим BHK. Например, действительное число мы должны трактовать как класс эквивалентности фундаментальных последовательностей рациональных чисел. Нетрудно записать какую-нибудь формулу

, определяющую фундаментальную последовательность рациональных чисел. И нетрудно определить, что последовательности рациональных чисел

и

"эквивалентны" (

) тогда и только тогда, когда их разность имеет пределом нуль. Но класс эквивалентности для

оказывается неразрешимым! Т.е. неизвестно, каким образом его можно "предъявить".



