Вычеты

[MChagall]

Необходимо вычислить интеграл

$$\int\limits_{\left\lvert z\right\rvert =3}^{}\frac{z^2 \sin(\frac{1}{z}) dz}{(z-1)(z-2)}$$

Особых точек три: 0, 1, 2. Все попадают в контур интегрирования. Значит, нужно вычислить три вычета.
Точки 1 и 2 - полюсы 1-го порядка. Получаем
для $z=1$
$\operatorname{res}=-\sin^2 1$
для $z=2$
$\operatorname{res}=4\sin^2 \frac{1}{2}$
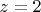
Может кто-нибудь посмотреть верно ли это?

А точка 0 - существенная? Как искать вычет в ней? Как коэффициент $c_{-1}$ в разложении по степеням $z$?

[Ms-dos4]

MChagall
Зачем вообще считать три вычета, когда можно считать один в бесконечно удалённой (учитывая, что у вас все особые точки в конечной части плоскости вошли в контур).

[thething]

MChagall в сообщении #1302004 писал(а):

для $z=1$
$\operatorname{res}=-\sin^2 1$

По какой формуле считали?

MChagall в сообщении #1302004 писал(а):

А точка 0 - существенная? Как искать вычет в ней? Как коэффициент $c_{-1}$ в разложении по степеням $z$?

Да. Синус легко раскладывается, дроби -- тоже.

Правда, я бы тоже перешел к бесконечной точке, она получается устранимая и для нее есть формула.

[MChagall]

thething в сообщении #1302012 писал(а):

По какой формуле считали?

Для полюса $a$ функции $f(z)=\frac{\varphi (z)}{\psi (z)}$ имеем $c_{-1}=\frac{\varphi (a)}{\psi '(a)}$

thething в сообщении #1302012 писал(а):

Синус легко раскладывается

Синус не могу. $\sin^2\frac{1}{z}=\frac{1}{2}-\frac{1}{2}\cos\frac{2}{z}$. И как косинус разложить?

thething в сообщении #1302012 писал(а):

дроби -- тоже.

Получилось

$$\sum\limits_{n=1}^{\infty}(1-\frac{1}{2^{n-1}})z^n$$

Правильно получилось?

thething в сообщении #1302012 писал(а):

для нее есть формула

$\operatorname{res} f = -c_{-1}$? Наталкиваюсь на разложение косинуса.

[Ms-dos4]

MChagall
1)Вычеты в полюсах вы сосчитали неверно, как вам уже выше сказали. Откуда у вас синусы "возвелись" в квадрат неясно.
2)По прежнему настаиваю на вычислении вычета в бесконечно удалённой. А синус раскладывается элементарно, известным с первого семестра рядом.

[MChagall]

Ms-dos4 в сообщении #1302020 писал(а):

Откуда у вас синусы "возвелись" в квадрат

Прошу прощения, опечатался в условии. Уже там синус в квадрате

$$\int\limits_{\left\lvert z\right\rvert =3}^{}\frac{z^2 \sin^2(\frac{1}{z}) dz}{(z-1)(z-2)}$$

Тогда верно вычеты найдены?

Ms-dos4 в сообщении #1302020 писал(а):

настаиваю на вычислении вычета в бесконечно удалённой

Вот так считать этот вычет $\operatorname{res} f = -c_{-1}$?

[thething]

Тогда верно.

Если $\infty$ -- устранимая особая точка, то ищите формулу вычета через предел

[MChagall]

thething в сообщении #1302047 писал(а):

формулу вычета через предел

${\operatorname{res}}\limits_{z=\infty} f(z)=-c_{-1}= \lim\limits_{z\to\infty}\bigl[f(\infty)-f(z)\bigr]z=\lim\limits_{z\to\infty}^{}\frac{-z^3\sin^2\frac{1}{z}}{(z-1)(z-2)}$. Верно?

[thething]

Да, верно..

А теперь представьте, что тот же ответ Вам надо было бы получать через ряды... Т.е. вычет в нуле представляет собой числовой ряд, сумма которого выражается через синусы единицы и одной второй, чтобы там все сократилось до нуля..

Кстати, не бойтесь рядов Лорана синуса и косинуса, они получаются из обычных рядов Тейлора

[MChagall]

$\lim\limits_{z\to\infty}^{}\frac{-z^3\sin^2\frac{1}{z}}{(z-1)(z-2)}=\lim\limits_{z\to\infty}^{}\frac{-z^3 \frac{1}{z^2}}{(z-1)(z-2)}=0$.
Вычисление самого предела вот так работает? (Использую что $\sin f(z) \sim f(z)$ при $f(z) \to 0$)
Получается, что исходный интеграл равен нулю, верно?

Ещё в задании необходимо обосновать существование интеграла. Разве то, что удовлетворяет условиям теоремы о вычетах не будет обоснованием?

[thething]

Все правильно..

Насчет обоснования, можно сказать, что интеграл существует, т.к. подынтегральная функция непрерывна на кусочно-гладкой кривой. Это на случай, если обосновать надо до вычисления. Если после вычисления, то да, теорема о вычетах все обосновывает.