Начал прорешивать упражнения по теме предел последовательности. Хочу проверить на верном ли я пути.
Прошу проверить мои решения(как если бы это было на экзамене), и правильность выбора упражнений(я выбирал наугад из Демидовича). Специальность Математика.
42. Доказать, что

есть бесконечно малая, указав для всякого

число

такое, что

при

, если

Решение.
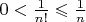
поэтому достаточно взять

49.

Числитель и знаменатель имеют предел, предел знаменателя не

, поэтому исходный предел будет равен отношению пределов числителя(

) и знаменателя(

)
Ответ

56.
![$\lim\limits_{n \to \infty}\left[\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\dots+\frac{1}{n(n+1)}\right] = \lim\limits_{n \to \infty}\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\dots+\frac{1}{n}-\frac{1}{n+1}\right) = \lim\limits_{n \to \infty}\left(1-\frac{1}{n+1}\right)=1$ $\lim\limits_{n \to \infty}\left[\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\dots+\frac{1}{n(n+1)}\right] = \lim\limits_{n \to \infty}\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\dots+\frac{1}{n}-\frac{1}{n+1}\right) = \lim\limits_{n \to \infty}\left(1-\frac{1}{n+1}\right)=1$](https://dxdy-02.korotkov.co.uk/f/1/8/8/188a180f56a42a5e73456cf736d9db1982.png)
Доказать
58.


Значит с некоторого

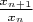
будет меньше любого заданного

, откуда


сколь угодно мало, исходя из того, что

сколь угодно велико, что можно доказать от противного:
пусть

ограничено, тогда у него есть точная верхняя граница

, поскольку граница точная, найдется

такое что

, что приводит к противоречию

.
Тогда
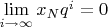
. Тогда и

сколь угодно мало.