Подскажите как лучше сделать в матричных вычислениях

[asteriks84]

Здравствуйте форумчане!
Прошу вашей подсказки в следующих матричных вычислениях, как лучше сделать и посчитать…
Имеем следующее:
$\[\left[ {\begin{array}{*{20}{c}} {{x_3}} \\ {{x_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{ - x_2^*} \\ {{x_2}}&{x_1^*} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{K_1}} \\ {{K_2}} \end{array}} \right]\]$ (обозначение * означает комплексное сопряжение), обозначим $\[{X_1} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{ - x_2^*} \\ {{x_2}}&{x_1^*} \end{array}} \right]\]$, получим $\[\left[ {\begin{array}{*{20}{c}} {{x_3}} \\ {{x_4}} \end{array}} \right] = {X_1} \cdot \left[ {\begin{array}{*{20}{c}} {{K_1}} \\ {{K_2}} \end{array}} \right]\]$.
Далее, $\[\left[ {\begin{array}{*{20}{c}} {{r_1}} \\ {{r_2}} \end{array}} \right] = X_1^T \cdot \left[ {\begin{array}{*{20}{c}} {{h_1}} \\ {{h_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{n_1}} \\ {{n_2}} \end{array}} \right]\]$, обозначим $\[{R_1} = \left[ {\begin{array}{*{20}{c}} {{r_1}} \\ {{r_2}} \end{array}} \right]\]$, $\[H = \left[ {\begin{array}{*{20}{c}} {{h_1}} \\ {{h_2}} \end{array}} \right]\]$, $\[N = \left[ {\begin{array}{*{20}{c}} {{n_1}} \\ {{n_2}} \end{array}} \right]\]$, получим $\[{R_1} = X_1^T \cdot H + N\]$.
Аналогично, $\[\left[ {\begin{array}{*{20}{c}} {{r_3}} \\ {{r_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_3}}&{{x_4}} \\ { - x_4^*}&{x_3^*} \end{array}} \right] \cdot H + N\]$, обозначим $\[{R_2} = \left[ {\begin{array}{*{20}{c}} {{r_3}} \\ {{r_4}} \end{array}} \right]\]$, $\[X_2^T = \left[ {\begin{array}{*{20}{c}} {{x_3}}&{{x_4}} \\ { - x_4^*}&{x_3^*} \end{array}} \right]\]$, получим $\[{R_2} = X_2^T \cdot H + N\]$.
Сведем, $\[\left\{ {\begin{array}{*{20}{c}} {{R_1} = X_1^T \cdot H + N} \\ {{R_2} = X_2^T \cdot H + N} \end{array}} \right.\, \Rightarrow \left[ {\begin{array}{*{20}{c}} {{R_1}} \\ {{R_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} H \\ N \end{array}} \right]\]$.
Значения $\[{R_1}\]$, $\[{R_2}\]$, $\[X_1^T\]$, $\[X_2^T\]$ - нам известны.
Методом Крамера попытаемся найти H и N.
$\[H = \dfrac{{\left[ {\begin{array}{*{20}{c}} {{R_1}}&1 \\ {{R_2}}&1 \end{array}} \right]}}{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right]}} = \dfrac{{{R_1} - {R_2}}}{{X_1^T - X_2^T}} \Rightarrow {\left( {X_1^T - X_2^T} \right)^{ - 1}} \cdot \left( {{R_1} - {R_2}} \right)\]$, и тут все получается. При подстановке комплексных чисел посчитанное значение H по данной формуле совпадает с значением H, заданным изначально. Что мне и нужно.
$\[N = \dfrac{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&{{R_1}} \\ {X_2^T}&{{R_2}} \end{array}} \right]}}{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right]}} = \dfrac{{{R_2} \cdot X_1^T - {R_1} \cdot X_2^T}}{{X_1^T - X_2^T}}\]$, а вот тут ничего не получается, как бы я не крутил… Вот тут мне и нужна Ваша помощь, как посчитать значение N.
Да, значение N можно конечно найти иначе. Зная посчитанное значение H, $\[N = {R_1} - X_1^T \cdot H\]$. Получается только так…

[asteriks84]

Формулу $\[N = \dfrac{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&{{R_1}} \\ {X_2^T}&{{R_2}} \end{array}} \right]}}{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right]}} = \dfrac{{{R_2} \cdot X_1^T - {R_1} \cdot X_2^T}}{{X_1^T - X_2^T}}\]$ читать формулой $\[N = \dfrac{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&{{R_1}} \\ {X_2^T}&{{R_2}} \end{array}} \right]}}{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right]}} = \dfrac{{X_1^T \cdot {R_2} - X_2^T \cdot {R_1}}}{{X_1^T - X_2^T}}\]$.

[vpb]

Применять формулы Крамера к системе, коэффициенты и неизвестные в которой --- матрицы, вообще говоря, нельзя, в следующем смысле. Пусть $A_{11}$, $A_{12}$, $A_{21}$, $A_{22}$ --- четыре $2\times2$ матрицы, $B_1$ и $B_2$ --- две $2\times1$ матрицы (т.е. столбца высоты 2). Мы можем рассмотреть систему "матричных уравнений"

$$ A_{11}X_1+A_{12}X_2=B_1 $$

$$ A_{21}X_1+A_{22}X_2=B_2, $$

где $X_1$, $X_2$ --- неизвестные $2\times1$ матрицы, которые мы хотим найти (а $A_{11},\ldots,B_2$ считаются известными). Возникает искушение формально написать "формулы Крамера"

$$ X_1=\frac{\begin{vmatrix} B_1 & A_{12} \\ B_2 & A_{22} \end{vmatrix} } {\begin{vmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{vmatrix} }=\frac{A_{22}B_1-A_{12}B_2}{A_{11}A_{22}-A_{21}A_{12}}$$

и для $X_2$ аналогично. Однако эти формулы не имеют смысла! Прежде всего, нельзя писать $A=\frac{B}{C}$, в случае, когда $B$ и $C$ матрицы (во-первых, у $B$ и $C$ могут быть несовместимые размеры. Во-вторых, даже если $B$ и $C$ --- квадратные матрицы одинакового размера, "левое частное" $C^{-1}B$ может не совпадать с "правым частным" $BC^{-1}$, поскольку умножение матриц, вообще говоря, не коммутативно. И вообще может быть так, что $C$ ненулевая, но не обратимая). Но даже если написать
$X_1=(A_{11}A_{22}-A_{21}A_{12})^{-1}(A_{22}B_1-A_{12}B_2)$
или
$X_1=(A_{22}B_1-A_{12}B_2)(A_{11}A_{22}-A_{21}A_{12})^{-1}$,
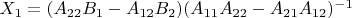
это всё равно будет неверно. Говоря короче, нельзя обращаться с матрицами так же, как с числами. Разве что при умножении двух матриц, разбитых на блоки. И то при этом надо следить за соответствием размеров блоков и за порядком умножения.

[asteriks84]

vpb, спасибо вам за разъяснения, действительно все так.
Подытожим с учетом некоторых полученных результатов.
Итак, мы имеем систему $\[\left\{ {\begin{array}{*{20}{c}} {{r_1} = {x_1}{h_1} + {x_2}{h_2} + {n_1}} \\ {{r_2} = - x_2^*{h_1} + x_1^*{h_2} + {n_2}} \\ {{r_3} = {x_3}{h_1} + {x_4}{h_2} + {n_1}} \\ {{r_4} = - x_4^*{h_1} + x_3^*{h_2} + {n_2}} \end{array}} \right. \Rightarrow \]$ $\[\left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{r_1}} \\ {{r_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}} \\ { - x_2^*}&{x_1^*} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{h_1}} \\ {{h_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{n_1}} \\ {{n_2}} \end{array}} \right]} \\ {\left[ {\begin{array}{*{20}{c}} {{r_3}} \\ {{r_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_3}}&{{x_4}} \\ { - x_4^*}&{x_3^*} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{h_1}} \\ {{h_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{n_1}} \\ {{n_2}} \end{array}} \right]} \end{array}} \right. \Rightarrow \]$ $\[\left\{ {\begin{array}{*{20}{c}} {{R_1} = X_1^T \cdot H + N} \\ {{R_2} = X_2^T \cdot H + N} \end{array}} \right. \Rightarrow \]$ $\[\left[ {\begin{array}{*{20}{c}} {{R_1}} \\ {{R_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} H \\ N \end{array}} \right]\]$
Задача найти значение $N$, при том, что $H$ тоже неизвестно.
Из системы нам удалось получить значение $H$.
$\[\tilde H = \dfrac{{\left[ {\begin{array}{*{20}{c}} {{R_1}}&1 \\ {{R_2}}&1 \end{array}} \right]}}{{\left[ {\begin{array}{*{20}{c}} {X_1^T}&1 \\ {X_2^T}&1 \end{array}} \right]}} = \dfrac{{{R_1} - {R_2}}}{{X_1^T - X_2^T}} = {\left( {X_1^T - X_2^T} \right)^{ - 1}} \cdot \left( {{R_1} - {R_2}} \right)\]$, и тут все получается. При подстановке комплексных чисел восстановленное значение $\[\tilde H\]$ по данной формуле совпадает с значением $H$, заданным изначально. Что мне и нужно.
Далее, подставив $\[\tilde H = {\left( {X_1^T - X_2^T} \right)^{ - 1}} \cdot \left( {{R_1} - {R_2}} \right)\]$ в $\[{R_1} = X_1^T \cdot H + N\]$, получим $\[{R_1} = X_1^T \cdot \left( {{{\left( {X_1^T - X_2^T} \right)}^{ - 1}} \cdot \left( {{R_1} - {R_2}} \right)} \right) + N \to \tilde N = {R_1} - \left( {{{\left( {X_1^T - X_2^T} \right)}^{ - 1}} \cdot \left( {{R_1} - {R_2}} \right)} \right)\]$ или $\[\tilde N = \left( {E - {{\left( {E - X_2^TX_1^{ - T}} \right)}^{ - 1}}} \right){R_1} + {\left( {E - X_2^TX_1^{ - T}} \right)^{ - 1}}{R_2}\]$ (данную формулу мне подсказали на форуме http://www.cyberforum.ru/algebra/thread2213949.html#post12255422).
Вроде как отлично! Что требовалось, то и получили и, что самое главное, все работает. Подставив комплексные числа все вычисляется идеально, за исключением случая, при котором $\[X_2^T = X_1^T\]$. У меня, к сожалению, один такой случай предполагается и поэтому не знаю, что предпринять…
Имеется такая таблица значений $\[{x_1}\]$, $\[{x_2}\]$, $\[{x_3}\]$, $\[{x_4}\]$, $\[{K_1}\]$, $\[{K_2}\]$ в зависимости от информационных сигналов $\[{c_1}...\,{c_4}\]$.


И вот в первом случае получается как раз, что $\[X_2^T = X_1^T\]$ и, следовательно, $N$, по той формуле вычислить не получается, а необходимо.