Делимость

[xjar1]

Есть задача

Цитата:

1. Делится ли число $11...1$ ($1$ повторяется $2001$ раз) на $37$?
2. Делится ли число $11...1$ ($1$ повторяется $1993$ раз) на $111111$?

Пункт 1 мне понятен, я вводил следующие обозначения: $E_1=3$, $E_2=3003$, $E_3=3003003$, ...
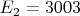
Понятно, что $37 E_1=111$, $37 E_2=111111$, $37 E_n=11...1$(1 повторяется $3n$ раз), Таким образом получаем, что $37 E_{667}=11...1$($1$ повторяется $2001$ раз), то есть делимость есть.

Во втором случае я поступал аналогично: $E_2=1000001$, $E_3=1000001000001$ , ...
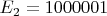
Обозачим через $I_n$ число 11...1, у которого 1 повторяется n раз.
Тогда $I_6 E_{332}=I_{1992}$, $I_6 E_{333}=I_{1998}$. Но ведь это все-таки не показывает то, что делимости нет.
Правильно ли я думаю: $I_{1993}=I_{1992}+10^{1993}$, а $10^{1993}$ не делится на $111111$, значит делимости нет.

Спасибо!

[provincialka]

Зачем такие большие числа?
$111111234=111111000+234$. Ясно, что первое слагаемое делится на $111111$. Поэтому делимость/неделимость числа $111111234$ такая же, как у $234$. То есть 6 единичек можно из числа вычеркнуть.

[waxtep]

xjar1 в сообщении #1299760 писал(а):

Правильно ли я думаю: $I_{1993}=I_{1992}+10^{1993}$

Или, $I_{1993}=10I_{1992}+1$. Можно Вашу процедуру в обратную сторону раскрутить, это тогда будет обычное деление "уголком"