Прошу проверить решение.
Есть такая задача (дело происходит на

-мерном

-гладком многообразии

).
Пусть

есть дифференциальная

-форма и

есть дифференциальная

-форма, не равная нулю. Доказать, что

представима в виде

тогда и только тогда, когда

.
В сторону

: внешне домножить равенство

на

справа и использовать

.
В сторону

: используем внутреннее умножение

дифференциальных форм, т. е. если

--- векторные поля, то
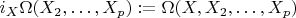
. Тогда из условия задачи

или
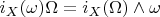
. Теперь надо выбрать векторное поле

так, чтобы

. Пусть

произвольная точка и в локальных координатах

вблизи точки

имеет место

. Одна из координат

не равна нулю в некоторой окрестности (с компактным замыканием)

точки

. Рассмотрим векторное поле

, где знак выбран так, чтобы

. Пусть окрестности

покрывают многообразие

и

--- соответствующее локально конечное разбиение единицы,

. Тогда векторное поле
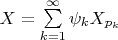
искомое. Осталось поделить равенство
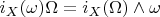
на

.
Правильно ли я склеил векторные поля?