У меня возникли трудности с такой задачей. Трудности заключаются в том, что я недостаточно хорошо, видимо, умею работать со смешанными мерами (я имею в виду смеси дискретных, непрерывных и сингулярных распределений). Конкретнее, есть такая задачка:
Пусть

и


случайные величины. Верно ли, что если условие
![$$\mathbb{E}[f(\xi)] = \mathbb{E}[f(\eta)]$$ $$\mathbb{E}[f(\xi)] = \mathbb{E}[f(\eta)]$$](https://dxdy-04.korotkov.co.uk/f/3/2/a/32ad38f6ccaf35f68d1ecdf4e5dd650482.png)
выполняется для любой непрерывной и ограниченной функции
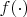
, тогда распределения

и

совпадают?
Мои продвижения заключаются в том, что я доказал, что это верное утверждение в случае, если:

и

абсолютно непрерывны;

и

дискретны;

дискретна, а

непрерывна.
Я также знаю, что рассматривать функции

недостаточно, так как существует пример различных случайных величин, все моменты которых совпадают.
На этом месте я, собственно, кончился, потому что не умею работать со смесями дискретных, непрерывных и, тем более, сингулярных случайных величин. Я полагаю, что ответ на эту задачу положителен, но никак не подступиться к решению. Вот допустим, я возьму меру, связанную с

, скажем,

и меру

, связанную с

. Как мне перевести данное в задаче утверждение на язык мер? Потому что я подозреваю, что ключ к решению состоит в этом. Заранее спасибо за любое содействие!