@Brukvalub
I thought too, but got an answer that everything is ok. If

then it is possible that min doesn't exist (I think it could be seen for a
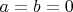
and

and of course

, so value of sum of integrals is

.
But if

why this would be a functional analysis problem? So u know now what's bothering me.