Ну по формуле включений-исключений
Да, в данном случае можно так. Однако, формула включений исключений, вообще говоря, дает не равенство, а неравенство (каламбур получился...). В полном виде она выглядит как

,
что в нашем случае приводит к неравенству
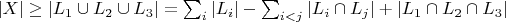
,
откуда

. Однако это рассуждение не доказывает, что конфигурация, для которой
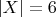
, действительно существует (так что может быть в принципе, что минимальное возможное значение для

--- это

,

, или что-то еще больше). Можете Вы предъявить такую конфигурацию в явном виде?
По второму вопросу Вы, собственно, ничего не написали, просто еще раз повторили то же утверждение (к тому же с опечатками, чего желательно избегать). Пока, пожалуй, оставим этот вопрос.
Скажите еще, а Вы какие-нибудь книжки по дискретной математике, комбинаторике и т.д. когда-нибудь читали? Если да, то какие?