AD писал(а):
Профессор Снэйп писал(а):
Так что очевидно, что индукция нужна лишь до него и не дальше, то есть по всем счётным ординалам.
Можно наивный вопрос? Так ведь
всех счетных ординалов несчетно. То есть нам нужно остановиться
раньше.

То есть найти такой
счетный ординал, дальше которого мы не пойдем. Я так это понимаю.
Я Вас не понимаю. Что значит "остановиться"?
Давайте распишем конструкцию подробно. Для каждого ординала

определим по трансфинитной индукции семейство

, состоящее из подмножеств

.
1) Пусть

--- семейство базовых борелевских множеств, то есть множеств вида
![$[a,b] \times [c,d]$ $[a,b] \times [c,d]$](https://dxdy-01.korotkov.co.uk/f/0/f/9/0f99b104bd0e67043af7a2e81e651c0782.png)
, где
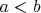
и

--- действительные числа.
2) Если

, то пусть

--- все (не более чем) счётные объединения, (не более чем) счётные пересечения и дополнения, аргументы которых берутся из

.
3) Если

--- предельный ординал, то

.
Легко показать, что найдётся ординал

, такой что

. Если

--- наименьший среди таких

, то

для всех

.
Ясно, что

есть в точности алгебра борелевских множеств. То, что

имеет мощность

, совсем очевидно. Принимая во внимание регулярность

(первый несчётный бесконечный кардинал), нетрудно показать, что

(из чего, в частности, сразу следует континуальность

). Будет ли

равно

или нет, я не знаю. Вполне возможно, что будет равно
